动态规划

[拼音]：dongtai guihua

[外文]：dynamic programming

研究具有广泛实际背景的一类决策过程的最优化问题。更一般地说，任何最优化问题，只要具备适当的结构，使得通过某种技巧可以对它建立起动态规划模型的，都是动态规划的研究对象。例如，求最短路径，制订工业生产中的最优资源使用计划、最优产品生产计划，制订企业管理中的最优库存方案，水库调度，化工生产中的最优工艺过程控制，核电站的最优关闭过程控制，航天器的轨道或姿态最优控制等，都是可以应用动态规划去解决其决策过程最优化问题的实例。所谓决策过程，是指人们在生产和科学实验活动中不断采取决策去控制其演变的过程。利用这类决策过程演变方面的特殊性质，动态规划发展了一套独特的解决决策过程最优化的方法。这一方法的基础是动态规划基本方程和最优性原理。

最初，动态规划的研究对象在数学上与古典变分法一样地属于泛函的极值问题。但古典变分法发展的实际背景是几何学和力学问题，问题的规模较小，结构较简单；而动态规划的背景则是运筹学和控制工程问题，问题的规模较大，结构较复杂。1953年R.贝尔曼总结了40年代末期以来对一些决策过程最优化问题的研究，发表专题论文“动态规划理论导引”，提出了动态规划这一学科名称，并阐述了最优性原理。以后，他以及其他的一些人陆续发表了一系列从理论上加以巩固和从内容上加以充实的论文。1957年，他的专著《动态规划》一书的出版，标志这一学科的创立。

动态规划模型

用动态规划解决决策过程的最优化问题，须先建立该过程的动态规划模型。实际的决策过程是随时间而演变的，所以时间参量是模型的一个组成部分。当决策是在离散的时段上采取时，时间参量是离散的，相应的决策过程是离散过程；当决策是在连续的时间上采取时，时间参量是连续的，相应的决策过程是连续过程。例如，在水库调度中，如果决策是一个时段（一天，一个月等）内的放水量，那么决策过程是离散的；如果决策是连续的放水流量，那么决策过程是连续的。在离散情况下，决策过程可划分成一系列的阶段，它也称为多段决策过程。决策过程从起始到终止的时段数或时间长度称为历程。历程可以是有限、无限或不定。时间参量的集以T表示，对于离散决策过程，它是有限集或可数集。

在决策过程中，状态起着描述过程的作用，意即所有各个时刻的状态一经确定，整个过程也就随之确定。当所有各个时刻如何作出决策的方式给定时，状态随时间的演变规律可能是确定性的，也可能是随机性的，相应的决策过程称为确定性决策过程或随机性决策过程。马尔可夫决策过程就是一种随机性决策过程。例如，在水库调度中，水库蓄水量可取作状态，若入库径流和放水都是确定性的，则相应的决策过程也是确定性的。一个决策过程，如要构成动态规划模型，其状态除了要起到上述的描述过程的作用外，还须满足下述的无后效性:给定某一时刻的状态，在此时刻后过程的发展不受此时刻以前状态的影响，过程的过去历史只通过当前的状态去影响它未来的发展。在一般情况下，状态是某一适当定义的状态集合X中的元素，集X称为状态空间。在特殊情况下，它是一个数或向量，称为状态变量。

在决策过程中，决策是影响或控制过程发展的外加因素，它是某一适当定义的决策集合U中的元素，集U称为决策空间。在特殊情况下，它是一个数或向量，称为决策变量。对于每一给定的t∈T和x∈X，决策必须在U的某一确定的子集U(t，x)内选取，此集称为时刻t和状态x下的允许决策集。例如，在水库调度中，当决策是一个时段的放水量时，U可以是不超过水库最大蓄水量与最大时段径流量之和的所有非负实数，U(t，x)可以是不超过t 时段水库蓄水量与径流量之和的所有非负实数。对于给定的t∈T，给出决策u随状态x变化的函数u(t，x)，相当于给出根据不同的当前状态作出不同决策的一套规则，称为决策规则。决策规则称为允许的，如它满足：对所有x∈X，u(t，x)∈U(t，x)。设T_s是与原过程的某一部分过程（或称为子过程）对应的时间参量集，函数族{u(t，x)｜u(t，x)∈U(t，x)，t∈T_s}称为此子过程的允许策略集；特别有，{u(t，x)｜u(t，x)∈U(t，x)，t∈T}为全过程的允许策略，对历程有限的离散过程，它是函数序列{u(t₀，x)，u(t₁，x)，…，u(t^N_-1，x)}。如果策略{u(t，x)|t∈T}中的u(t，x)不依赖时间而成为u(x)，则称它为平稳策略，它意味着在任何时刻所选取的决策规则都是相同的。在这种情况下，可以用决策规则u(x)表示策略。

给定时刻t的状态x和子过程的时间参量集[t，t┡](t┡>t)上的策略，则对于确定性（随机性）决策过程，时刻t┡的状态（状态概率分布）就完全确定。这种前后状态与策略的关系，称为状态转移规律。例如，在水库调度中，设x_t是时段t的状态(时段t开始时的蓄水量)，u_t是该时段的放水量，g_t是该时段的入库径流量，x_t+1是下一时段t+1的状态，则有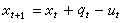，此方程表达了水库调度的状态转移规律。对于不同类型的决策过程，其状态转移规律具有不同的表现形式。对于确定性离散决策过程，它可以由方程表示，称为状态转移方程，上述水库例子是它的一个特例。对于随机性离散决策过程，它可由转移概率P_t(x_t+1｜x_t，u_t)表示。对于确定性连续决策过程，它可由含有状态和决策变量的微分方程表示。对于随机性连续决策过程，它则可由适当形式的随机微分方程表示。

为了对决策过程进行最优化，须先提出衡量过程好坏的准则。在传统的动态规划中，此准则是一数量指标，是一定义在原过程和所有子过程上的实值函数，称为指标函数。例如，对于用于发电的水库，指标的一种选法是调度过程的总发电量。设此过程由N个时段组成，每一时段t 的发电量υ_t(t=1，2，…，N)为该时段开始时蓄水量x_t与该时段放水量u_t的函数，则指标函数为k=1，2，…，N。对于一般的确定性离散决策过程，此函数的形式为V(t，x_t，u_t，x_t+1，u_t+1，…)，t=1，2，…，在动态规划模型中，要求它满足下列递推关系

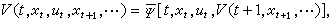
根据问题的不同特点，可以提出形式很不相同的各种指标。例如，对于无限的过程，可以提出无折扣或带折扣的累计指标，某种意义下的对时间平均的指标等；对于随机性决策过程，可以提出以概率、以极值、以数学期望值或以方差表示的指标等。

总之，一般说来，决策过程的动态规划模型包括下列组成部分：时间参量集、状态空间、决策空间、容许决策集的族、状态转移规律、指标、初始和终止条件等。决策过程的最优化，就是要在容许策略集内求出策略，使之能满足初始和终止条件，并且在某种意义上使指标达到最优值。

动态规划基本方程

由动态规划模型的构成可见，作为动态规划研究对象的决策过程具有如下性质：采用时间与状态作为参量，它可以形成结构相同的一族决策过程。动态规划的基本思想就在于从最优化的角度去利用这项性质，把原来的某一决策过程最优化问题，看成采用时间与状态作为参量的某一族决策过程最优化问题中的一个族元，通过对族的研究得出最优性条件、最优策略和最优过程的结构及其求解方法。换言之，就是把某单一的最优化问题嵌入到具有结构与特征不变的一族最优化问题中去。在这个意义上来说，动态规划的基本思想是不变嵌入原理的一种特殊形式。动态规划基本方程就是在这基础上得出的最优值函数所满足的方程。这里最优值函数的定义如下:设t为决策过程的某一时刻，x为该时刻状态，p[t，t^ƒ]是由该时刻起到终止时刻t^ƒ止的子过程上的策略， V (t，x，p[t，t^ƒ])为此子过程上的指标值，则 这里的上(下)确界是在相应的允许策略集内取的。如在此集合内最优策略存在，sup(inf)就变成max(min)。依照决策过程的类型不同，动态规划基本方程取不同形式，下面列出若干重要形式：

（1）历程确定、有限的离散决策过程

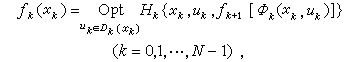(1)

ƒ^N(x^N)满足边界条件。

(1)式中Opt依情况表示sup，inf，max，min;H_k在确定性决策过程中表示指标递推函数ψ[t_k，x_k，u_k，V]。

（2）历程不定或无限的离散决策过程

，　　　(2)

ƒ(x)满足边界条件。

（3）历程有限的连续确定性决策过程

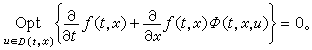(3)

这里决策过程的状态转移规律由微分方程凧＝φ(t，x，u)确定，指标是终端函数。

最优性原理

决策过程的最优策略的基本性质的表述。最初它被用作建立动态规划理论的基础。下面是R.贝尔曼原来的表述：不论初始状态与初始决策为何，对于先前的决策所造成的状态而言，下余的那些决策必构成一最优策略，是最优策略具有的性质。在最简单的问题中，最优性原理的含意和证明都是很简单的。例如，在最短路径问题中，可以这样去理解最优性原理：若由始点S到终点T的最短路径通过中间点 M(见图

)，则点M在此路径所截下的后半段MT 对于以M点作为始点的路径来说必是最短的。否则，就能找到从M到T的另一条更短的路径，把它与原来路径的前半段SM相接，就得到由S到T的比原来的路径更短的路径，于是得出矛盾。对于复杂的问题，情况自然没有这样简单；在各种不同的决策过程最优化问题中，最优性原理是否成立，必须根据问题的条件进行论证。动态规划理论的内容之一就是对所建立的各种决策过程的模型论证最优性原理。另一方面，一般说来，最优性原理的成立与动态规划基本方程的成立并不彼此等价，在许多情况下，可以证明动态规划基本方程是相应模型的决策过程最优性的充分必要条件，但是从最优性原理本身的表述可见它仅表达策略最优性的必要条件。从实际求解的角度来看，动态规划基本方程也是更基本的工具。

算法

在动态规划中最基本的算法是上述方程(1)的数值求解程序，因绝大多数应用问题在构成动态规划模型后，解析解不存在而须用数值方法求解时，都归结为此方程的数值求解，这就是所谓的动态规划常规算法。常规算法的主要困难在于，在方程(1)中对k进行逆推计算时，必须把ƒ_k(x_k)存于内存中，所需容量与x_k的维数成指数增长关系，因而此算法对高维问题是不现实的。目前已提出克服此困难的方法主要有函数逼近法、拉格朗日乘子法、结构分解法、松弛法、状态增量动态规划法、微分动态规划法等，但是困难未获根本解决。

方程(2)、(3)与(1)不同，它不是函数组的递推关系，而是单一函数ƒ(x)的函数方程，动态规划为之提出了两种解法。一是值迭代法，一是策略迭代法。值迭代法中，所谓值是指指标最优值。任选迭代初始的值函数 ƒ₀(x)，对于第n次迭代所得值函数，由下式求第n+1次值函数

，

这样得到两序列{ƒ_n(x)}和{u_n(x)}，在一定条件下，n→时，ƒ_n(x)→ƒ(x)，u_n(x)→u(x)，而u(x)为最优策略。

动态规划与古典变分法及最大值原理的关系

古典变分法与动态规划所研究的问题的区别，除背景不同外，前者主要考虑开集的局部极值问题，后者则考虑任何集内的全局极值问题。动态规划所能处理的极值问题，在约束集和目标函数形式这些方面都可以远比古典变分法复杂。另一方面，古典变分法的主要结果都可用动态规划的方法推导出来。例如，在相应的数学模型和古典变分法中通常的假定下，可以证明，动态规划基本方程(3)就是古典变分法中哈密顿-雅可比方程，而是哈密顿函数。因此方程 (3)也称为哈密顿-雅可比-贝尔曼方程。

对于适当构造的数学模型，可以证明，动态规划里的指标最优值函数ƒ（x）与Л.С.庞特里亚金的最大值原理中的哈密顿函数H存在着确定的关系，例如，对于博尔萨问题，其中L是指标积分内的被积函数，φ是状态微分方程凧＝φ的右端部分，其变元应按最优状态轨线和最优决策取值。而且，动态规划基本方程正好就是最大值原理中哈密顿函数在容许决策集上取最大值的这一基本条件。

简史

在动态规划的初步理论建立之后，大部分研究工作是结合运筹学和控制工程两方面的实际应用而进行的。在确定性问题方面，还对动态规划与古典变分法的关系以及它与庞特里亚金的最大值原理的关系进行了研究。在随机性问题方面　，1960年R.A.霍华德发表了“动态规划与马尔可夫过程”，1962年和1965年，D.布克韦尔先后发表了“离散动态规划”和“带折扣的动态规划”，这些工作使R.贝尔曼在动态规划中所开始研究的马尔可夫决策过程得到重要的发展，使之成为动态规划的一个分支。

初期，动态规划的若干基本方面不够成熟，随着理论的发展和应用的需要，对动态规划的理论基础的研究逐渐发展，这里的中心问题包括：最优性原理和动态规划基本方程的适用范围及其在动态规划理论中的地位和作用，建立动态规划理论的公理化体系的可能性等。基于实际应用的需要，寻找适于在计算机上使用的动态规划数值计算方法以及与此有关的理论，则是动态规划研究工作的另一重要方面。在20世纪60年代中后期提出的状态增量动态规划、微分动态规划以及非序列动态规划的二级最优化问题的研究，都属于这方面的工作。目前，除上述各方面在继续发展外，动态规划还从理论上不断扩展它的研究领域，例如，在决策方面，已出现把容许决策扩展成广义函数的工作；在指标方面，则已出现把指标函数扩展成向量指标与其他更一般的非数量指标的工作。

参考书目

1. R. Bellman，Dynamic Programming，Princeton Univ.Press， Princeton， 1957.
2. R.A.霍华特著，李为政等译：《动态规划与马尔柯夫过程》，上海科学技术出版社，上海，1963。(R.A.Howard，Dynamic Programming and Markov Processes， John Wiley & Sons，New York， 1960.)
3. G.L.Nemhauser，Introduction to Dynamic Program-ming， John Wiley & Sons， New York， 1967.
4. D.J.White，Dynamic Programming，Olive and Boyd，Edinburgh， London， 1969.
5. S.E.Dreyfus and A. M.Law，The Art and Theory of Dynamic Programming，Academic Press， New York， 1977.