[拼音]:fanhan weifen fangcheng
[外文]:functional differential equation
除了理想的情形以外,任何具有反馈的动力系统总是存在滞后现象;用传统的常微分方程去描述物理系统只是一种近似,而且是有条件的,这就需要考虑带有各种滞后量的微分方程,诸如微分差分方程,各种具有复杂偏差变元的微分方程,有滞后量的积分微分方程,等等。泛函微分方程是这一类方程的概括和抽象。
最早的泛函微分方程来自1750年L.欧拉提出的几何问题:求一曲线使之与其渐缩线相似。这种曲线便满足一个特殊的泛函微分方程,此后不断从各个学科中提出这类问题。到20世纪40年代为止,主要是研究微分差分方程的解析解。50年代开始探讨稳定性理论,1959年H.H.克拉索夫斯基在函数空间之间建立解映射,从而确立了滞后型泛函微分方程。70年代初,J.黑尔与A.克鲁兹分离出一类广泛的中立型方程。1978年赫尔与加藤敏夫共同奠立了具有无穷滞后的泛函微分方程。以后又有对其他类型的中立型泛函微分方程的研究。
给定实数r≥0,区间[-r,0]到n维实(或复)线性空间Rn的连续映射全体记为C([-r,0],Rn),简记为C,C中元素φ 的范数取为 则C 为巴拿赫空间且具有一致收敛拓扑。若t0∈R,A≥0,且x∈C([t0-r,t0+A],Rn),则对任何t∈[t0,t0+A],记xt(θ)=x(t+θ)(-r≤θ≤0),显然xt∈C。若D吇R×C,给定映射ƒ:D→Rn,则
则C 为巴拿赫空间且具有一致收敛拓扑。若t0∈R,A≥0,且x∈C([t0-r,t0+A],Rn),则对任何t∈[t0,t0+A],记xt(θ)=x(t+θ)(-r≤θ≤0),显然xt∈C。若D吇R×C,给定映射ƒ:D→Rn,则
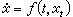 (1)
(1)
叫做D上的滞后型泛函微分方程,记为RFDE(ƒ)。(1)中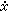 为右导数。若存在t0∈R,A >0 使得
为右导数。若存在t0∈R,A >0 使得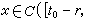
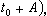
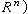 ,(t,xt)∈D,且当
,(t,xt)∈D,且当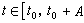 )时x(t)满足(1),则称x(t)为(1)之解。若t0∈R ,φ∈C 给定,且x(t;t0,φ)为(1)之解。则当
)时x(t)满足(1),则称x(t)为(1)之解。若t0∈R ,φ∈C 给定,且x(t;t0,φ)为(1)之解。则当 时称x为过 (t0,φ)的解。由此可以建立两种解映射:
时称x为过 (t0,φ)的解。由此可以建立两种解映射:
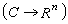 及
及  。而且一般地说解空间是无穷维的。当r=0时(1)退化为常微分方程,解映射为
。而且一般地说解空间是无穷维的。当r=0时(1)退化为常微分方程,解映射为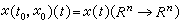 ,解空间是有限维的。二者截然不同,通常解的存在惟一性,稳定性,周期解的存在性都不等价。但常微分方程的许多方法可以推广而用于泛函微分方程,得出大量相应的结果。当然,这种推广往往是困难的,有时甚至是不可能的。
,解空间是有限维的。二者截然不同,通常解的存在惟一性,稳定性,周期解的存在性都不等价。但常微分方程的许多方法可以推广而用于泛函微分方程,得出大量相应的结果。当然,这种推广往往是困难的,有时甚至是不可能的。
对(1)有如下的存在定理:给定开集D吇R×C,ƒ:D→Rn是连续的,若(t0,φ)∈D,则必存在(1)过(t0,φ)的解x(t,t0,φ)即在t0具有初值φ0。若加上ƒ 在D中关于φ满足李普希茨条件(见常微分方程初值问题),则解存在且惟一。同样也可得到解关于参数和初始数据的连续依赖性与可微性的相应定理。关于解的开拓,有一个普通的结果:若x为(1)在[t0-r,b)上的不可开拓解,则对任何紧集K嶅D存在一个t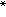 使得t
使得t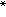 ≤t≤b时(x,xt)唘K。
≤t≤b时(x,xt)唘K。
若(1)右端不显含t,则方程为
 (2)
(2)
称之为自治系统。设ƒ:C→Rn是连续的,并且是C的有界闭集到Rn中有界集的映射。记x(φ)为(2)过(0,φ)且定义于[-r,∞)上的惟一解,则  对任何t、s≥0成立。因而定义了一个动力系统。集
对任何t、s≥0成立。因而定义了一个动力系统。集
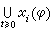 叫做过φ的轨线。
叫做过φ的轨线。 。叫做у
。叫做у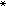 (φ)的ω 极限集,
(φ)的ω 极限集,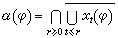 叫做у
叫做у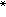 (φ)的α 极限集。相应于常微分方程的已知结果,有对(2)的一个解x,若存在常数 m>0 使得 t∈[t0-r,∞] 时│x(t)│<m,则у
(φ)的α 极限集。相应于常微分方程的已知结果,有对(2)的一个解x,若存在常数 m>0 使得 t∈[t0-r,∞] 时│x(t)│<m,则у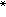 (x0)包含于C的紧集之中,若t≥-r时│x(t)│<m,则ω(у
(x0)包含于C的紧集之中,若t≥-r时│x(t)│<m,则ω(у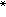 (x0))是非空的连通紧不变集,且t→∞时 dist(xt,ω(у
(x0))是非空的连通紧不变集,且t→∞时 dist(xt,ω(у (x0)))→0。
(x0)))→0。
作为(1)的特殊情形,考虑线性方程
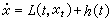 , (3)
, (3)
>h(t)∈LL1((t0,∞)中的局部L可积函数),L(t,φ)是φ的线性泛函。由里斯定理,存在一个 n×n矩阵函数η(t,θ),它是二元可测的,对每个t当θ∈[-r,0]时是有界变差的,使L(t,φ)表示为
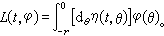
任何t∈R,φ∈C,设存在函数 m(t)∈LL1(-r,∞),使|L(t,φ)|≤m(t)‖φ‖,那么可以证明(3)过(t0,φ)的解x(t0,φ,h)存在且惟一,并且x(t0,φ,0)关于φ是线性的,x(t0,0,h)关于h是线性的。由于L(t,φ)是线性的以及解的惟一性可以推出

易法(见初等常微分方程)还可把x(t,φ,h)表示为常数变易公式,即 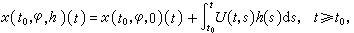 式中
式中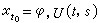 是方程
是方程
 的解
的解
U 称为基本解阵,I是n×n单位阵, Ut(·,s)(θ)=U(t+θ,s)(-r≤θ≤0)。
若(3)右端不显含t,则得线性自治系统
 (4)
(4)
记x(φ)为过(0,φ)的解,由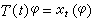 定义算子T(t):C→C,则映射族{T(t):t≥0}为C上之强连续半群。群之无穷小生成元由
定义算子T(t):C→C,则映射族{T(t):t≥0}为C上之强连续半群。群之无穷小生成元由 ,定义。A的定义域D(A)在C中稠密且A之值域R(A)在C中。A可由下式给出:
,定义。A的定义域D(A)在C中稠密且A之值域R(A)在C中。A可由下式给出:
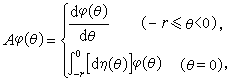
式中φ 在[-r,0)上有连续导数,η(θ)为[-r,0]上的有界变差函数阵。对任何φ∈C有 。所以,对任意的φ∈D(A)有
。所以,对任意的φ∈D(A)有
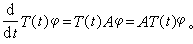
当然,线性系统的各式扰动问题也有相应的结果。
若(2)中h(t)呏0,L(t+ω,φ)=L(t,φ)(ω=常数>0)即周期线性系统,此时弗洛奎特理论的相应推广存在困难。即使最简单的纯量方程 夻(t)=(sint)y(t-2π)也可以证明它不存在周期为2π的变换可使之化为自治系统。
设(1)满足ƒ(t,0)呏0,t∈R+=[0,∞),
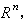 是连续的,这里
是连续的,这里 若对任何ε>0和t0≥0,存在δ(ε,t0)>0,使(1)之解x(t,t0,φ)对一切t≥t0,φ∈Cδ时有xt(t0,φ)∈Cε,则称(1)的零解x=0为稳定的。否则,为不稳定的。若以上的δ 不依赖于t0,则称为一致稳定的。若对任意的ε>0,t0≥0,存在δ1(t0)和T(ε,t0)使当
若对任何ε>0和t0≥0,存在δ(ε,t0)>0,使(1)之解x(t,t0,φ)对一切t≥t0,φ∈Cδ时有xt(t0,φ)∈Cε,则称(1)的零解x=0为稳定的。否则,为不稳定的。若以上的δ 不依赖于t0,则称为一致稳定的。若对任意的ε>0,t0≥0,存在δ1(t0)和T(ε,t0)使当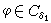 且t>t0+T(ε,t0)时
且t>t0+T(ε,t0)时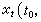
 则称(1)的零解为渐近稳定的。若δ1和T不依赖于t0,则称为一致渐近稳定的。对线性自治系统,可以分析特征根的分布并且应用第一近似理论得出非常类似于常微分方程的稳定性定理。行之有效的李亚普诺夫第二方法(见常微分方程运动稳定性理论)则有两种格式。其一是所采用的V函数仍为Rn→R(或R×Rn→R)的纯量函数,但需要拉祖米欣条件:对正定函数V(t,x),x∈Rn,设(1)满足V(σ,x(σ))≤V(t,x(t))(t≥t0,t-r≤σ≤t)的解x(t)(或包含解的曲线族)的集合SR非空,全导数
则称(1)的零解为渐近稳定的。若δ1和T不依赖于t0,则称为一致渐近稳定的。对线性自治系统,可以分析特征根的分布并且应用第一近似理论得出非常类似于常微分方程的稳定性定理。行之有效的李亚普诺夫第二方法(见常微分方程运动稳定性理论)则有两种格式。其一是所采用的V函数仍为Rn→R(或R×Rn→R)的纯量函数,但需要拉祖米欣条件:对正定函数V(t,x),x∈Rn,设(1)满足V(σ,x(σ))≤V(t,x(t))(t≥t0,t-r≤σ≤t)的解x(t)(或包含解的曲线族)的集合SR非空,全导数 在SR上为常负的,则可保证零解是稳定的。若方程右端含有带滞后量的导数项(即对中立型方程),仅有上述的拉祖米欣条件还不能判定稳定性。可引进条件:当 V(σ,x(σ))≤N(t),有|凧(σ)|≤k(N(t)),t-r≤σ≤t,其中函数N(t)是正值函数,k:R+→R+连续且严格增加,k(0)=0;再加上拉祖米欣条件,得到稳定性判定方法。这种类型的结果统称拉祖米欣型定理。其二是采用李亚普诺夫泛函,
在SR上为常负的,则可保证零解是稳定的。若方程右端含有带滞后量的导数项(即对中立型方程),仅有上述的拉祖米欣条件还不能判定稳定性。可引进条件:当 V(σ,x(σ))≤N(t),有|凧(σ)|≤k(N(t)),t-r≤σ≤t,其中函数N(t)是正值函数,k:R+→R+连续且严格增加,k(0)=0;再加上拉祖米欣条件,得到稳定性判定方法。这种类型的结果统称拉祖米欣型定理。其二是采用李亚普诺夫泛函, ,令
,令

式中xt+h(t,φ)是(1)过(t,φ)的解,设(1)中ƒ:R×C→Rn使R×(C的有界子集)映入Rn之有界集、u、v、w:R+→R+是连续非减函数,u(s)、v(s)当s>0时是正的,且u(0)=v(0)=0。若存在连续泛函V:R+×C→R使得
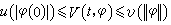 ,
,

则(1)的零解一致稳定。若加上s>0时w(s)>0,则零解一致渐近稳定。这类结果在国内外有大量推广。
20世纪70年代有两个新发展。一是r取-∞,则同一个(1)式表示具无穷滞后系统,可以得出与上述内容大体平行的一些结果。二是中立型方程,设Ω吇R×C为开集,ƒ:Ω→Rn,D:Ω→Rn给定且连续。D在0处是“原子的”,则
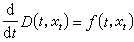 (5)
(5)
叫做中立型泛函微分方程(NFDE(D,ƒ)),D叫做(5)的差分算子。当D关于φ为线性时, 所谓在0处“原子的”,是指det[η(t,0)-η(t,0_)]≠0。若D为非线性的,则条件加之于Dφψ(弗雷歇导数)。对(5)的基本理论与稳定性理论已有一系列结果。
所谓在0处“原子的”,是指det[η(t,0)-η(t,0_)]≠0。若D为非线性的,则条件加之于Dφψ(弗雷歇导数)。对(5)的基本理论与稳定性理论已有一系列结果。
- 参考书目
- J. Hale,Theory of Functional Differential Equations,Springer-Verlag, New York, 1977.