[拼音]：wuxianqun
[外文]：infinite group
元素个数为无限的群。拓扑群，李群，（无限）典型群，代数群，算术群，都是无限群。
20世纪30年代以来，无限群研究有了迅速的发展。与研究其他的代数系统一样，无限群论的最终目的是刻画所有的群。基于有限群论积累的许多成果，无限群论开始研究的都是那些接近有限群的群类，以及在有限群论中研究过的那些类型，诸如交换群、幂零群、可解群等。所研究的问题大致有两类，一类是把关于有限群的结果推广到尽可能广泛的无限群上去；一类是无限群所特有的一些问题，例如关于自由群、群的本原类、伯恩赛德问题等。
关于无限交换群已在交换群中述及，因此以下提到的无限群均指非交换群。
划分出一些群类是研究群的首要问题，常用的划分群类的方法有下列几种。
（1）链条件，是指对子群适合极大(小)条件，即该群中任意非空子群集都有极大(小)者。
（2）局部系概念，如果群G的某个子群集L满足条件a.L中子群的并集等于整个群G;b.L中任意两个子群含于L中的某个子群内，那么L称为局部系。如果G中存在一个由具有性质p的子群组成的局部系，就说群G局部地有性质p或局部p群。于是就有局部有限群、局部幂零(可解)群类。
（3）正规系（不变系）的概念，是熟知的正规列、不变列的推广。可用它们来定义所谓RN 群、RI 群等。
（4）要求对某些构成方法，诸如“取子群”、“取商群”、“取直积”、“取扩张”等是封闭的，也可划分出一些群类。最重要的本原类就是关于“取子群”、“取商群”、“取直积”封闭的群类。
作为把一类无限群化归为对有限群的研究的例子，是切尔尼科夫定理：一个群是对子群有极小条件的可解群，当且仅当它是对子群有极小条件的可除交换群借助有限可解群的扩张。作为推广有限群论的定理的例子，是R.贝尔的结果:局部正规群(指它的任意有限子集含于它的某个有限正规子群中)的两个西洛p子群是局部共轭的。
无限群论中所特有的局部定理，回答了一个群局部地具有性质p是否它本身也具有性质p的问题。例如对于RN群有局部定理:局部RN群(局部RI 群)是RN群(RI 群)。Α.И.马尔采夫给出了一个证明局部定理的统一方法，即后来称作马尔采夫-塔尔斯基完备定理中所指出的方法。
群的构成方法是群论的重要课题之一。尤其是有限群的扩张问题，研究用生成元和定义关系给出的群，以及群的直积、群的自由积和自由群等。以自由群为例，任取集合x＝{xα，α∈I}，另作一符号集
，令M=x∪x -1，考虑M字，即由M中元素组成的形式有限序列：
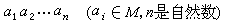。 (1)
为方便起见，引入空字即不含任何元素的字。如果有α∈I，α，b∈M，使集合
，那么(α， b)称为一个逆对。令G是一切满足以下条件的M字全体。
（1）在字(1)中任意两个相邻元素αi，αi+1不组成逆对；
（2）规定G中两个元素α1α2…αn和b1b2…bm 之乘积:若(αn， b1)不是逆对，则为G中M字α1…αnb1…bm；若(αn， ，b1)，…，(αi，b n-j+1)都是逆对，而(αj-1，bn-j+2)不是逆对，则为G中M字
α1…αj-1bn-j+2…bm
（此时可能出现空字或只有αj或只有bj的情况）。易知在此运算下空字是单位元，而G中每一元都有逆元。可以证明这个乘法适合结合律，因而G是一个群，称之为以x为自由生成元集的自由群。
自由群G有如下的泛性质：任给一群H，任给集x（G的自由生成元集）到集H的一个映射φ，则φ可扩充为群G到群H的一个同态映射。由此可得，任意群H都是某个自由群的商群。关于自由群有重要的尼尔森－施赖埃尔定理：自由群的任意异于单位的子群本身也是自由群。它的推广是对一些群的自由积的子群的刻画，即著名的库洛什定理：若
，而H是群G的子群，则群H有自由分解
，其中F是自由群，而任一Bβ在G中共轭于某个Aα的一个子群。群G称为其子群Aα（异于单位子群）的自由积，是指①集合
生成整个群G，即对任意g∈G有
(2)
② 若这些元素αi都异于单位元而(2)中相邻的两个元素没有同属于一个Aα者，则这样的表示法是惟一的。此时记作
。
群论中有一些著名问题，例如，在具有有限个生成元和有限个定义关系式的群中，讨论两个元素是否相等的所谓恒等问题；讨论两个元素是否共轭的所谓共轭问题；讨论这样两个群是否同构的所谓同构问题；讨论有限生成的周期群是否为有限群的所谓伯恩赛德问题。E.C.戈洛德对伯恩赛德问题给出了反例。于是退而提出了有界伯恩赛德问题:具有k个生成元且满足恒等式xn=1的群（都记作B(n，k)）是否为有限群。已经证明，B(6，k)都是有限群，而当奇数n≥665，k>1时，总有是无限群的B(n，k)，后者即∏.С.诺维科夫和 С.И.阿江的著名定理。无限群论在研究一般代数系统中起着示范作用。它本身也在继续发展。