有限群

[拼音]：youxianqun

[外文]：finite group

具有有限多个元素的群。群论的重要内容之一。其所含元素的个数，称为有限群的阶。有限群可分为两大类：可解群与非可解群（特别包括非交换单群）（见群、有限单群）。

可解群

如果有限群G 之合成群列的每个商群G_i-1/G_i（称为G 的合成商因子）是交换群，那么有限群G 称为可解群。易知，若G的合成商因子G_i-1/G_i是交换群，则必为素数阶的循环群。所谓G的合成群列，是指在G 中由有限多个子群组成的降链如，使得G_i是G_i-1的极大正规子群，即，且凡满足G_i<H<G_i-1的H不再是G_i-1的正规子群。G的任意两个合成群列是等价的，意即如果与是G的任意两个合成群列，那么必有s=r，且r个商群H₀/H₁，H₁/H₂，…，H_r-1/H_r（即H_r-1）分别与r个商群G₀/G₁，G₁/G₂，…，G_r-1/G_r(即G_r-1)除次序外是两两互相同构的。易证，由合成群列G=G₀>G₁>…>G_r=1所成的每个商群是单群。

在群G中由有限多个正规子群组成的降链使G_i为真包含于G_i-1内的G 之极大正规子群(即G_i-1/G_i是G/G_i的极小正规子群)，称为G的主群列。G的任意两个主群列是等价的。其等价定义与合成群列的等价定义相同。

有限群有合成群列或主群列存在，且任意两个合成群列或主群列是等价的。这就是若尔当-赫尔德-施赖埃尔定理。凡是阶等于p^αъ的群恒为可解群，其中p、是互异的素数，α、b是非负整数。这就是著名的伯恩赛德定理。而W.费特、J.汤普森在20世纪60年代初期又证明了有限群中长期悬而未决的一个猜想，奇数阶的群一定是可解群，因而有限非交换单群的阶必为偶数。

西洛性质

有限群理论中一个经典而重要的结果是著名的拉格朗日定理:有限群G的阶│G│等于G的子群H的阶│H│与 H在G内的指数│G:H│的乘积，即│G│=│H│·│G:H│。但是，并非对│G│的任何因数d，G一定有阶为d的子群。例如，四次交错群A₄的阶为12，而A₄没有6阶子群（见置换群）。当│G│的因数是p^k形的数即一素数p的k次幂时，则G必有阶为p^k的子群。这就是有名的西洛第一定理。若除尽│G│的p的最高次幂是p^m，其中p是素数，m是自然数，则G的p^m阶子群称为西洛p子群。所谓西洛第二定理，其意为：

（1）G中任两个西洛p子群在G内是共轭的；

（2）G中西洛p子群的个数N，必满足N呏1(modp)，且为任一西洛p子群的正规化子在G内的指数；

（3）G中凡是阶为p^k的子群必为某西洛p子群的子群。进一步有关于有限可解群的西洛基定理:G为可解群的充分必要条件是G有一组西洛基S₁，S₂，…，S_r，使G=S₁S₂…S_r。所谓西洛基，是指当G的阶（素因数分解）时，G的一组西洛p_i子群S_i，i=1，2，…，r，且，使。可解群的西洛基往往不止一组，但是，可解群的任意两组西洛基S₁，S₂，…，S_r与p₁，p₂，…，S_r是等价的，即在G中必有元素g使。阶为素数幂的群，习惯上称为p群。西洛子群都是 p群。有限可解群可以表为 p群之积。西洛第一定理和第二定理统称为西洛定理。在有限可解群中可得到西洛定理推广的结果:有限群G为可解群的充分必要条件是，只要有分解│G│=mn，(m，n)=1，G就有阶为m的子群；当G是可解群时，凡是阶为m的子群必互为共轭，若m₁│m，则G中凡是阶为m₁的子群必为G中至少一个阶为m的子群的子群。这样的m阶子群，通常称为可解群G中的霍尔π子群。

所谓群的π 性质，意即西洛性质的推广。西洛性质是西洛定理的同义语， 即如果有限群G的阶|G|=g，h│g，(h，g/h)=1，h为素数幂，那么G至少有一个h阶子群，且任意两个h阶子群是共轭的，而G中凡是以h的因数为阶的子群，一定是G中某个h阶子群的子群。P.霍尔去掉上述条件中的“h为素数幂”而设“G是可解群”并得到了同样的结论。于是，根据P.霍尔的这一思想方法，将“h为素数幂”改为其他条件来进行探索的工作颇多。例如，“h为素数幂”改为“G包含一个h阶幂零子群”，仍得到相应的结论，即古典的西洛定理推广到含有h的一切素因数的集合π上所得的结果。

幂零群

当可解群 G的西洛基中诸西洛子群都是正规子群时，则可解群G称为幂零群。幂零群是可解群中的一个子类。有限群G为幂零群的充分必要条件是，G可表为p群的直积。p群自身当然是幂零群。除了这个充分必要条件外，还有几个互为等价的充分必要条件，其中最重要的是，G有上中心列或下中心列。所谓上中心列，是指G有长为m的子群列，使，且其中 Z₁(G)为 G 的中心Z(G)，而递归地给出Z_k+1(G)使 Z_k+1(G)/Z_k(G)是商群G/Z_k(G)的中心。由G的限性可知，必有某自然数k使，因此当m≥k时， 恒有Z_m(G)=Z_k(G)。特别地，有某m使Z_m(G)=G。所谓下中心列，是指G有长为n的子群列。设H、K是G的任意两个子集，[H，K]表示由形如 的元素所生成的G的子群，即[H，K]=<[h，k]│h∈H，k∈K>，于是[H，K]=[K，H]。当[x₁，…，x_n]定义后，再递归地定义。同样，对G的子集H₁，…，H_n也作类似的定义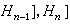，且当任意x_i∈G(i=1，2，…，n)时，则定义，因此，且。易知。从G的有限性可知，有某自然数k使。因此当m≥k时恒有K_m(G)=K_k(G)。特别地，有自然数 n使K_n+1(G)=1。有限群的上中心列和下中心列两者同时存在，且其长相等， 此时G必为幂零群，称为n类幂零群。因而，1类幂零群就是交换群。由此可知，幂零群是介于交换群与可解群之间的一类群。幂零群有下中心列，可解群则有换位群列。G为可解群的充分必要条件是，G有换位群列。所谓换位群列，是指G的子群列，式中为的换位子群，即，而n是某一正整数。此时G也称为n步可解群。1步可解群就是交换群。

p群

在有限群的研究中，p群具有重要的意义。互不同构的pⁿ阶群究竟有多少个，是一个古老而艰难的问题。迄今只解决了当p为奇素数且n≤6时以及当p=2且n≤7时pⁿ阶群的个数问题。关于p群方面的工作颇多，其中由P.霍尔发表的计数原理与正则 p群是奠基性的工作。所谓计数定理，例如，设｜G｜=pⁿ，S_k(G)表示G中p^k阶子群的个数，其中0≤k≤n。当S_k(G)=1(1<k<n)时，则G必是循环群;当S₁(G)=1时;则G或为循环群或可能为所谓广义四元数群，后者仅在p=2及n≥3时可能出现；对于0≤k≤n，有S_k(G)呏1(modp)。特别地，设G为非循环群，p>2则对于1≤k≤n-1有（库拉科夫定理）。又令C_k(G)表pⁿ阶群G中p^k阶循环子群的个数。设G是非循环群，p>2，则对于1<k<n有C_k(G)呏0(modp)（米勒定理）。两者以及其他的一些计数定理皆可用P.霍尔的计数原理来证明。在这方面华罗庚、段学复早在20世纪40年代就曾一起进行过一些工作。例如，设p>2，｜G｜=pⁿ，p^n-α为G中元素之阶的最大数，且n≥2α+1，华罗庚于1945年证明了对于α+1≤m≤n-α有C_m(G)=p。段学复于1948年证明了对于 2α+1≤m≤n，S_m(G)与1，1+p，1+p+p²、1+p+2p²四者之一同余mod p³。所谓正则 p群，是指具有如下性质的p群G:对于G的任意元素α、b恒可找到r个元素с₁，с₂，…，с_r，使每个с_i∈<α，b>┡＝[<α，b>，<α，b>]即每个с_i在由α、b生成的群之换位子群内，且有，其中自然数r随元素α、b决定。交换p群、阶不超过p^p的p群以及幂零类小于p的p群，都是正则p群;换位子群为循环群而p为奇素数的p群、凡非单位元的阶等于p的p群，也都是正则p群。正则p群在p群中有众多例子。但非正则p群也是存在的，例如，p²次对称群中西洛p子群就是p^p+1阶非正则p群。

扩张

研究有限群的一个重要方法。设A、B是已知的两个群，如果作一群G，使得AG，且商群G/A≌B，那么群G称为B基于A的扩张。一般，B基于A的扩张不是惟一的，例如，A与B的直积A×B是B基于A的一个扩张，而A与B的半直积也是B基于A的扩张。所谓A与B的半直积为G，是指G=AB，AG，且A∩B=1（即B为A的补子群）。A与B的半直积又称为A的分离扩张。B基于A的扩张为 A与B的半直积的一个充分条件是：A的阶与B的阶互素。这就是著名的舒尔-扎森豪斯定理。当B为循环群时，很容易决定扩张的构造。例如，m阶循环群基于n阶循环群的扩张，必为G＝<α，b>，有定义关系αⁿ=1，b^m=α^t，b^-1αb=α_r使满足r^m呏1(mod n)及t(r-1)呏0(modn)。因为有限群有合成群列，这里，G_i/G_i+1是单群。因此，G_r-1是单群，且G_r-2是G_r-2/G_r-1基于G_r-1的扩张。若得知G_r-1的构造，则可借助于扩张理论得知G_r-2的构造，从G_r-2的构造以及G_r-3是G_r-3/G_r-2基于G_r-2的扩张可知G_r-3的构造，如此继续进行下去，则终究可得知G的构造。由此可见，研究单群与扩张理论是有限群研究的根本课题。

转移

研究有限群的一个重要方法。设 A是有限群G的任一个子群，将G表为A的右陪集的并集，即，于是│G:A│=n。令A┡=[A，A]，并作商群A/A┡，且用表以G关于A┡的右陪集为元素的集合，若令，则知的每一元素可惟一表为μ=αμ_i，即惟一决定数码i及交换群A/A┡的一个代表元素α，α∈A，因此，对G的每一元素g，有，式中(1_g，2_g，…，n_g)为(1，2，…，n)的一个排列，且α_i，g∈A。作矩阵M_g=(α_i，g)使其第i行第i_g列交叉处的元素为α_i，g(i=1，2，…，n)，而其他处的元素均为0。易证。由此可知，映射g →M_g是G的一个同态映射，称为G的单项表示。因A/A┡是交换群，故可引进行列式，简记为。于是，映射也是G的同态映射，即G到A/A┡内的同态映射，称为G到子群A的转移。利用转移方法可得出许多重要结果。例如，有限群G的西洛p子群p若包含于其正规化子的中心之内，即，则有G=Np，N G，N∩p=1。这就是又一个著名的伯恩赛德定理。由此可知，阶为合数的单群只有两种可能：或为阶被12整除的单群或为阶被8整除的单群。

超可解群

它是介乎幂零群与可解群之间的一类有限群。所谓超可解群，是指有限群G有一个有限多个正规子群的递降列使每个商群G_i-1/G_i为循环群。因此，超可解群是可解群的特例，又是幂零群的推广。判断有限群G 为超可解群有许多等价的充分必要条件，其中常见的有：

（1）G的每个极大子群的指数为素数；

（2）G的主群列的商因子皆为素数阶的循环群；

（3）G的每一子群H(≤G)都有一切可能阶的子群。

参考书目

1. W. Burnside，Theory of Groups of Finite Order， 2nd ed.，Cambridge Univ. Press， Cambridge， 1911.
2. D.Gorenstein，Finite Groups， Harper and Row， New York， 1968.
3. B.Huppert， Endliche Gruppen，I，Springer-Verlag，Berlin， 1967.