[拼音]：suxing zengliang lilun
[外文]：incremental theory of plasticity
塑性力学中用应变增量表述弹塑性材料本构关系的理论，也称塑性流动理论。弹塑性材料的本构关系与应变和应力的历史有关，因而弹塑性材料的应力和应变之间没有一一对应关系。为了反映变形的历史，本构关系须以增量形式给出。
研究简史1870年法国的A.J.C.B.de圣维南首先提出，在塑性变形过程中，塑性材料的应变增量的分量同应力偏量的分量成比例。此后，法国的M.莱维于1871年和德国的R.von米泽斯于 1913年各自独立地得到三维情况的普遍的本构方程。1924年德国的L.普朗特提出，对某些弹塑性问题，应考虑弹性应变增量。A.罗伊斯于1930年将普朗特的思想推广到三维应力问题，并建立了弹塑性体的普朗特-罗伊斯本构方程。此后，美国的W.普拉格和D.C.德鲁克又给出了具有强化性质的材料的本构方程。
增量形式的本构方程莱维和米泽斯认为，材料在屈服后即发生塑性流动。根据他们的理论，本构方程为：
de孆＝dλsij， （1）
式中de孆为塑性应变偏量增量的分量；sij为应力偏量的分量； dλ为非负的比例系数，它不仅和材料性质有关，而且和塑性变形历史有关。式（1）称为莱维-米泽斯方程。
当弹性应变和塑性应变相比不可忽略时，应将弹性应变和塑性应变同时考虑，相应的普朗特-罗伊斯本构方程（简称普朗特-罗伊斯方程）为：
， （2）
式中deij、de
、de孆分别为总的、弹性的和塑性的应变偏量增量的分量;G为材料的剪切模量(见材料的力学性能)。
德鲁克根据塑性变形过程中附加应力对应变增量所作的功非负这一假设，在应变增量主轴和应力主轴重合的前提下，得出塑性应变增量的矢量和屈服面（见屈服条件）法线方向重合的结论。如果屈服面的外法线方向用屈服函数f的梯度矢量
来表示，则有：
， （3）
式中σij为应力分量；dε孆为塑性应变增量分量。在几何上，式（3）表示塑性应变增量的矢量与屈服面正交。在塑性变形体积不可压缩的假设下，塑性应变增量的分量和塑性应变偏量增量的分量是相等的，即
dε孆＝de孆。 （4）
f在式(3)中起着塑性势能的作用。如果取f为米泽斯屈服函数，则由式（3）可以得到式（1）。式（3）称为与屈服条件相关联的塑性流动法则，也叫正交法则。
对于强化材料，塑性变形通常改变屈服面的大小、形状和位置（见强化规律），这时要用加载面（又称后继屈服面）来判断一点的应力状态是否达到了塑性状态。如果材料在从一个塑性状态变化到另一个塑性状态的过程中产生新的塑性应变，则这个过程称为塑性加载（简称加载）；如果从某个塑性状态转到某一弹性状态的过程中并不产生新的塑性变形，则这个过程称为卸载；如果材料从一个塑性状态转到另一个塑性状态，而应力增量不引起塑性应变的变化，则这个过程称为中性变载。由于在加载、卸载和中性变载过程中弹塑性介质的本构方程具有不同的形式，所以必须给出一个判断加载、卸载和中性变载的准则。对强化材料，塑性加-卸载准则可表示为：
（5）
式（5）的几何意义是，在应力空间中，应力增量矢量指向加载面外侧为加载，指向内侧为卸载，与加载面相切则为中性变载。由于只有当
才可能有新的塑性变形，因此可将流动法则中的dλ和df用下式联系起来：
dλ＝hdf， （6）
式中h称为强化函数，它与应力、应变、塑性变形历史和强化模型的选取有关。根据式（3）和式（5）并考虑弹性应变增量，便可得到普拉格-德鲁克的弹塑性强化材料的本构方程（简称普拉格-德鲁克方程）：
，
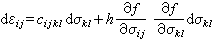式中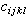
为材料的弹性常数；重复下标表示约定求和。
在实际应用中，使用普朗特-罗伊斯方程或普拉格－德鲁克方程求弹塑性问题的解析解是很困难的，但近年来它们在金属结构的有限元分析（见有限元法）中得到广泛的应用。在金属加工和成型问题的计算中，由于塑性变形比弹性变形大得多通常略去弹性变形，因而莱维-米泽斯方程得到了广泛的应用。
1951年，德鲁克提出一个塑性的基本公设，称为德鲁克公设。它可叙述为：处于某一初始应力状态下的材料单元，借助一个外部作用，在原有的应力状态上缓慢地加上一组附加的应力，然后卸除，则在附加应力作用过程中，以及在附加应力作用与卸除的一个循环内，外部作用所作的功是非负的。此外，苏联的A.A.伊柳辛也提出一个以应变表述的塑性基本公设。用这些公设可以证明塑性流动的正交法则，导出加-卸载准则，以及证明加载面的外凸性。这两个公设对塑性力学的发展起了推动作用。