斯托克斯流动

[拼音]：situokesi liudong

[外文]：Stokesˊflow

不可压缩流体的低雷诺数流动，又称蠕动流，是英国科学家G.G.斯托克斯首先从理论上进行研究并给出解析解的，故得名(见彩图)。

在斯托克斯流动中，雷诺数很小，惯性力远小于粘性力，粘性力起主导作用，因此可以完全忽略惯性力。此时流体力学基本方程组采取下列形式：

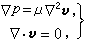　　　　　　　　(1)

式中v和p为流体的速度矢量和压力；μ为动力粘性系数。

对于平面和轴对称运动，存在流函数Ψ，它满足下列方程：

墷²墷²Ψ＝0（平面运动），　　　　　(2)

D²D²Ψ＝0（轴对称运动），　　　　(3)

式中墷²(也记为Δ)为拉普拉斯算符；D²为广义的斯托克斯算符，它们在直角坐标(x，y，z)、柱坐标(r，φ，z)和球坐标(r，φ，θ)系中分别采取下列形式：

，

，

。

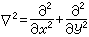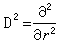
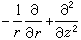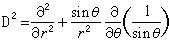解出流函数后，便可容易地求出速度和压力。

求解线性方程(2)和(3)的方法主要有以下几种：

（1）分离变量法　适当选取曲线坐标系，使边界恰好是坐标面。于是，可用分离变量法求方程(2)的精确解。圆球、双圆球、椭球的无界绕流问题以及单个圆球垂直地向一无界平面运动的问题等都可用分离变量法求精确解。

（2）反射法　这是一种逐次逼近的近似解法。以双球问题为例。设第一个球不存在时，第二个球的流场是零级近似。然后将第一个球的流场对第二个球的反射作为一级近似，如此继续下去。第n级近似是n-1级近似对第二球的反射并使之满足无滑移条件。利用反射法可以处理多种问题。对于圆球间隔较圆球半径大得多的情形，反射法给出收敛快的结果。但是当圆球间隔接近圆球半径时，反射法需要高级近似而且收敛得非常慢。因此对于干扰很强的情形，此法不适用。

（3）强干涉方法　由方程(2)和(3)的一般形式的普遍解，应用反射、匹配和配置等技巧满足流动边界条件，通过级数截断和解线性代数方程组可以得到近似解。实践证明这种方法即使对于干扰很强的情形也收敛得很快。利用它可以处理圆球串的无界斯托克斯流、圆管内多球的斯托克斯流和圆球从半无穷空间通过小孔进入另一半无穷空间等问题。

（4）奇点分布法　将奇点离散地或连续地分布在某线段或物面上，然后利用配置法令解在物面上有限个选定点上满足边界条件就可求出奇点的强度分布。这种方法可以用来解决任意物体的无界和有界绕流问题（见奇点分布法）。

斯托克斯流动在化学工程、土木工程、采矿工程、生物工程等领域内有着广泛的应用，近年来它的研究发展迅速。

参考书目

1. J.Happel and H. Brenner， Low　Reynolds　NumberHydrodynamics，　with　 Special　Application　to Particulate Media，Prentice-Hall，Englewood Cliffs，New Jersey，1965.