[拼音]：jiasudu
[外文]：acceleration
表征单位时间内速度改变程度的矢量。一般情况下，加速度是个瞬时概念，它的常用单位是厘米/秒2、米/秒2等。
在最简单的匀加速直线运动中，加速度的大小等于单位时间内速度的增量。若动点的速度v1经t秒后变成v2，则其加速度可表示为：
。
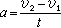动点Q做一般空间运动时， 速度矢量的变化和所经时间Δt的比，称为Δt时间内的平均加速度（图1），
记为a平：
。
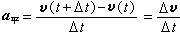当时间间隔Δt趋于零时，平均加速度的极限称为瞬时加速度(图1)，简称加速度，记为a：
。
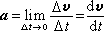因而加速度的严格定义为：加速度矢量等于速度矢量对时间的导数，其方向沿着速端图的切线方向并指向轨迹的凹侧。关于加速度产生的原因，可参见牛顿运动定律。
加速度在各坐标系中的表示方法如下：
直角坐标系可用于表示点的空间曲线运动、平面曲线运动和直线运动的加速度。
（1）空间曲线运动
式中ax、ay、az 为动点加速度a 在直角坐标轴上的投影；
、
、
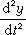为动点位置坐标对时间的二次导数；α、β、γ为加速度a与坐标轴x、y、z的夹角。
（2）平面曲线运动
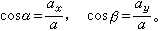
（3）直线运动 取动点的轨迹直线为x 轴，x为动点坐标，则其加速度为
。这里a和v 都可用标量表示；符号正或负表示加速度沿x 轴的正向或反向。当a与v符号相同时，运动是加速的；符号不同时，运动是减速的。若a为常数，称作匀变速直线运动。通过积分并代入初始条件（t＝0时，x＝0，v＝v0），可得出匀变速直线运动的速度和路程公式：
。
可用于表示点的平面曲线运动的加速度。和速度类似，加速度在极坐标系中亦可分解为横向加速度a嗞和径向加速度ar，它们分别等于：
。
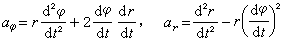可用于表示空间曲线运动和平面曲线运动的加速度。
（1）平面曲线运动 可将加速度分解到轨迹的切向和法向。曲线坐标S表示动点至轨迹上任选原点O的孤长（图2）。
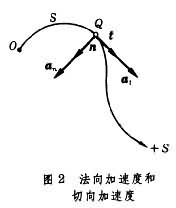
在某点Q处，沿S增加的切线方向定为切线的正向，并以t表示Q处的单位切向矢量。再将垂直于t、 指向轨迹凹侧的方向定为正法向，并以n表示单位法向矢量。加速度a可分解为切向加速度at和法向加速度an：
a＝at+an＝att+ann，
式中
，它们是加速度沿轨迹切向和法向的投影，皆为标量，但an总是正量，即法向加速度总是指向轨迹曲线的凹侧。此外，ρ表示轨迹曲线在Q点的曲率半径。以正法线上一点C为圆心，以CQ＝ρ为半径，作一圆，称为曲率圆。在Q点附近，曲率圆上的微弧段可近似地代替轨迹曲线的弧段。
在动点Q以匀速v沿半径为r的圆周运动时，其切向加速度at＝0，法向加速度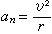
，指向圆心。故a＝an，又称向心加速度（图3）。向心加速度是向心力（如绳的拉力等）产生的，正是这个力连续地改变着速度的方向，迫使动点做匀速圆周运动。
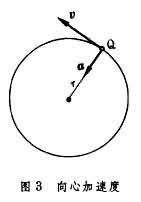
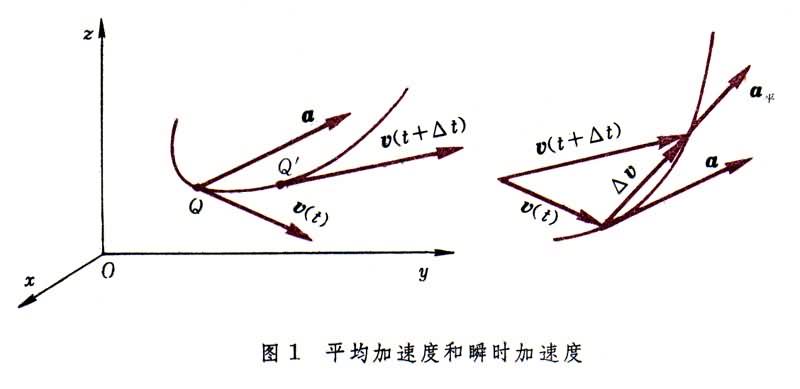
（2）空间曲线运动 如图4所示，在点的运动轨迹OQL上，确定Q为运动的始点，沿路程S的增加方向定义切向单位矢量t。在轨迹曲线上任取两点Q1和Q2，则Q、Q1、Q2三点可决定一平面。当Q1和Q2向Q趋近时，上述平面的极限平面称为曲线在 Q点的密切面。密切面内垂直于t、指向曲线凹侧的单位矢量n称为法向单位矢量。曲率圆(圆心为O┡，半径为ρ)位于密切面内。依右手坐标系规则，从t和n可以确定第三个单位矢量b。曲线上每一点的三个单位矢量t、n、b确定该点的自然轴系，它刻画曲线在该点的几何特性。n所在的直线称为Q点处曲线的主法线;b所在的直线叫Q点处曲线的副法线。Q点的加速度沿自然轴系各轴的分量分别为切向加速度at，法向加速度an和副法向加速度ab，而ab恒等于零。以ρ表示曲率半径，则有：
a＝at+an+ab＝att+ann，
式中
。
