图论

[拼音]：tulun

[外文]：graph theory

数学的一个分支。它以图为研究对象。图论中的图是若干给定的点及连接两点的线所构成的图形，这种图形通常用来描述某些事物之间的某种特定关系，用点代表事物，用连接两点的线表示相应两个事物间具有这种关系。因此这种图中点的位置、线的长短曲直是无关紧要的。

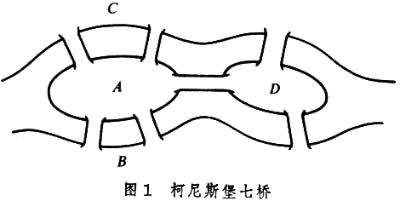
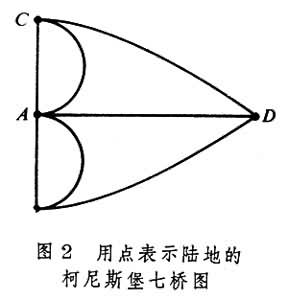
图论起源于著名的柯尼斯堡七桥问题。在柯尼斯堡(今苏联加里宁格勒)的普莱格尔河上有七座桥，将河中的两个岛和河岸连结，如图1所示，要寻找一条路线，经过每座桥只一次而能回到出发点。1736年，L.欧拉用点表示陆地，用连结两个点的线来表示桥，以图2代替图1，提出了第一个图论问题：对给定的图，是否存在一条路线，使得通过每条线正好一次而能回到起点。他证明了：当且仅当，图是连通的以及每个点都与偶数条线相关联时，才存在上述的路线(所谓的欧拉圈)。图2虽然是连通的，但是每个点都与奇数条线相关联，所以并不存在欧拉圈。

1847年，G.R.基尔霍夫在建立电网络理论时，以图G（图4）代替电网络N（图3）

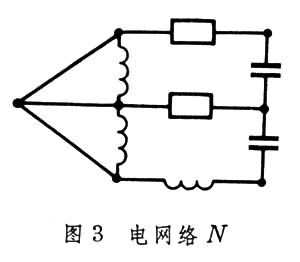
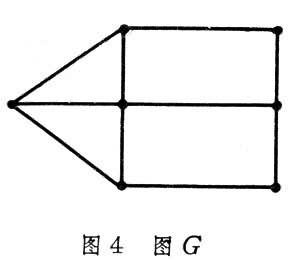
提出了“连通图”、“树”、“支撑树”等基本概念。

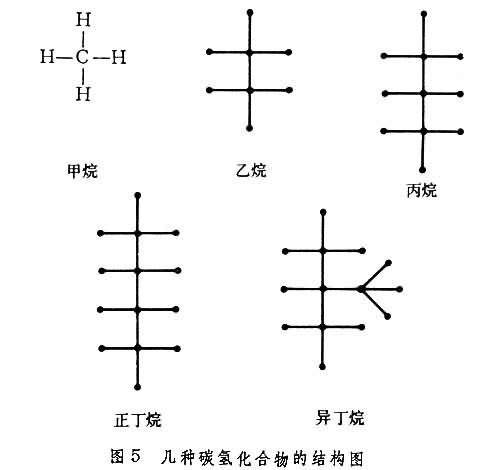
1857年，A.凯莱在研究饱和碳氢化合物(C_nH_2n+2)同分异构体的数目时，独立地提出了“树”的概念。他把这一类化合物的计数问题，抽象为计算某类树的个数问题。在这类树中，要求关联到每点的线的条数是1或4，树上的点对应于一个氢原子或一个碳原子（图5）。这一问题是图的计数理论的起源。

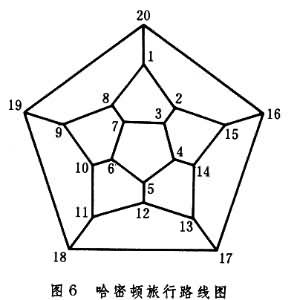
1859年，W.R.哈密顿提出了一种叫做“旅行世界”的游戏，把一个正十二面体的20个顶点看作20个城市(图6)。要寻找一条沿着多面体的边走的旅行路线，经过每个顶点正好一次，最后回到出发点，例如，1→2→3→…→20→1就是一种走法。将这个问题推广到一般图上，即对给定的图是否存在一条路线，使得通过每个点正好一次，最后回到起点（所谓的哈密顿圈）。这就是哈密顿问题。由于运筹学、计算机科学以及编码理论中的很多问题，都可化为哈密顿问题，从而引起了广泛的注意，但是至今只得到一些关于哈密顿圈存在的充分条件。例如，若关联到每个点的线的条数不少于图的点数的一半，则必存在哈密顿圈。

1936年，D.柯尼希写出了第一本图论的书。近三十年来，图论的广泛应用，促进了图论自身的发展。例如，W.T.塔特等发展了由H.惠特尼首先提出的拟阵理论，C.伯奇等发展了超图理论，P.爱尔特希等发展了极图理论。此外，代数图论、拓扑图论等方面也有了很大的进展。

图的定义

在图论中， 所谓图G， 是指由两个集合V（G）和E（G）所组成的集合，并记作G =（V，E），其中

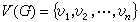称为点集，它的元素υ称为G的点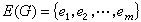；称为边集，它的元素e称为G的边，是V(G)的某些点对。若e=(υ_i，υ_j)是一条边，则点υ_i和υ_j称为互相邻接，或称为e的两个端点。同时把边e和点υ_j(或υ_j)称为互相关联的。 若两条边e_h和e_k都关联于某一点υ，则边e_h和e_k称为互相邻接。一个具有n个点的图，如其每一对点都是互相邻接的，则此图称为完全图，记作K_n，如图7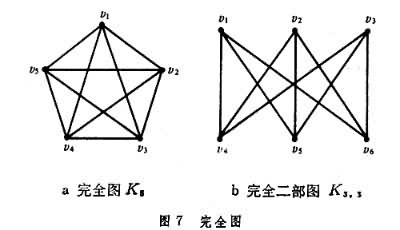

中的K₅。若图的点集V能够划分成两个子集V₁和V₂，使得图中每条边都关联于V₁和V₂中的各一个点，则称这种图是一个二部图。若从一个二部图的V₁和V₂中各取一点所成的任何点对，都是图的边，则称这个二部图为完全二部图。假设此时V₁中的点数为r，V₂中的点数为s，则记此完全二部图为K_r，s如图7中的K_3，3。

关联于某一点υ的边的数目称为该点的度，记作d(υ)。通常把各点的度中最小者记作δ，最大者记作Δ。

若两个图G＝(V，E)和G┡=(V┡，E┡)中的V和V┡之间存在保持邻接性质的一一对应关系，则称G 和G┡是同构的，记作G≌G┡。例如，图8

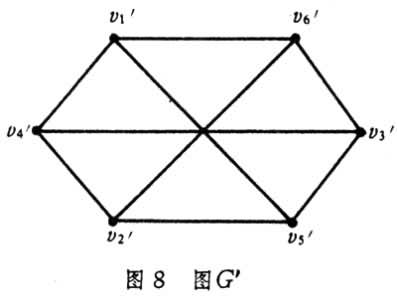
中的G┡和图 7中的K_3，3是同构的。若两个图G＝(V，E)和G┡=(V┡，E┡)有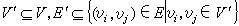，则称G┡是G的一个子图。从G中减去点υ以及所有关联于υ的边后所得的子图，记为G-υ。从G中减去边e（保留其端点）后所得的子图，记为G-e。

连通度

若一点序列 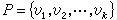中相继的两点所构成的点对(υ_i，υ_i+1)都是图中的边，则称p为一条联结υ₁和υ_k的链。而 υ₁和υ_k称为链p 的两个端点。一条两个端点相重合的链，称为圈。一个图，若任何两点之间，至少存在一条联系它们的链，则称之为连通图。否则，称为不连通图。一个无圈的连通图称为树。设图G的子图G┡含有G的所有的点，如果G┡是树，那么称G┡为G的一个支撑树。设G不是完全图，使G变成不连通图所需要减去的最少点数，称为G的点连通度，记作k(G)。对完全图K_p，取κ(K_p)=p-1。设G至少含有两个点，使G变成不连通图所需要减去的最少边数，称为 G的边连通度，记作λ(G)。对G中任意两条联结点u和υ的不同链，若除了u和υ之外再没有其他的公共点，则称它为联结u和υ的两条点不相交的链。若两条联结u和υ的链没有公共边，则称其为联结u和υ的两条边不相交的链。K.门杰于1927年获得一个有关图的点连通度的著名定理：图 G中每对点之间至少有κ(G)条点不相交的链。对边连通度也有相似的结果:图G中每对点之间至少有λ(G)条边不相交的链。这是1956年由L.R.福特和D.R.富尔克森发现的。

无关数与覆盖数

若 x是点（或边）的一个子集合，其中的点(或边)两两互不邻接，则称x为图的一个点（或边）无关集。在各点(或边)无关集中，其所含的点（或边）数达到最大者，称为最大点（或边）无关集，而它所含的点（或边）数，称为图的点（或边）无关数，记作β₀（或β₁）。点（或边）的一个子集合S，若使得图中任意一个边（或点），至少与S中一个点（或边）相关联，则称S为图的一个点(或边)覆盖集。在各点(或边)覆盖集中，所含的点（或边）数达到最小的覆盖集，称为最小点（或边）覆盖集，其所含的点（或边）数称为图的点（或边）覆盖数，记作α₀(或α₁)。当G是二部图时，设V₁中的点代表工人，V₂中的点代表工作，边(u_i，υ_j)代表工人u_i熟悉工作υ_j，则G的边无关数β₁表示能同时将工人安排到熟悉的工作上的最大数目。柯尼希于1931年获得了一个关于图的边无关数的著名定理:若G是二部图，则G的边无关数等于点覆盖数(即β₁=α₀)。对任意的连通图G，T.加莱于1959年发现如下的简明关系式:α₀+β₀=n;当δ>0时，α₁+β₁=n，式中n是图的点数。因此，当G是二部图时，点无关数等于边覆盖数（即β₀=α₁）。对二部图求参数α₀、α₁、β₀、β₁的问题，都可化为线性规划问题。点（或边）覆盖集和点（或边）无关集分别都对应于相应线性规划问题的基本可行解。其中求α₀(或α₁)的线性规划问题和求β₁(或β₀)的线性规划问题，恰巧互为对偶规划。因此，柯尼希定理是一个组合形式的对偶定理(见线性规划)。门杰定理也可以通过线性规划对偶定理来证明。假如一个边无关集又是边覆盖集，则称它是图的一个1-因子。D.W.霍尔于1935年，首先对二部图给出了存在1-因子的充分必要条件。1947年，塔特给出了任意图存在1-因子的充分必要条件。在此基础上，他还发展了图的因子理论。

色数

图的每一个点（或边）染一种颜色，使得染同一种颜色的点（或边）都互不邻接所需要的最少颜色种数，称为图的点（或边）色数。记作λ（或λ┡）。显然，边色数不能小于图的最大度，即λ┡≥Δ。V.G.维津于1964年证明了λ┡≤Δ+1。关于点色数，R.L.布鲁克斯在1941年已获得如下的结果：若G是连通图，它既不是一个奇数点的圈，也不是一个完全图，则λ≤Δ。当G是二部图时，λ┡=Δ，λ≤2。假设V₁中的点代表工人，V₂中的点代表设备， 而边(u_i，υ_j)代表工人u_i要求使用设备υ_j一天。如果在同一天内，每个工人只能使用一种设备，而每种设备只能被一个人使用，那么G的边色数λ┡表示最少要λ┡天后才能满足各工人对各种设备的要求。

平面图

若用几何的点和线来表示一个图 G的点和边，在平面上画出G时每两条线，除端点外，内部互不相交，则称G是一个平面图。例如，印刷电路板上的线路图就是一种平面图。完全图 K₅和完全二部图K_3，3是两个分别使点数和边数最少的非平面图。平面图的边把平面划分为若干个连通的区域。每个连通的区域称为平面图的一个面。欧拉公式 ƒ₀-ƒ₁+ƒ₂=2反映了平面图的点数ƒ₀、边数ƒ₁及面数ƒ₂的关系。设(u，υ)是G的一条边，若在这条边上增加一个新的点ω，用两个边(u，ω)和(ω，υ)来代替(u，υ)时，称边(u，υ)被ω 细分。两个图，若能从同一个图通过一系列的边的细分而得到，则称这两个图同胚。例如，任何两个圈都同胚。图9

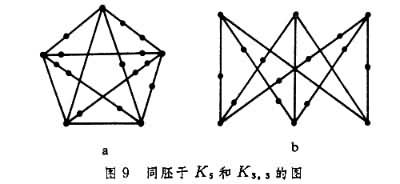
中是两个分别同胚于K₅和K_3，3的图。1930年，K.库拉托夫斯基首先给出了平面图的特征:一个图G是平面图，当且仅当，G中不含有同胚于K₅或K_3，3的子图。这是图论中著名的定理之一。平面图的研究与四色问题以及拓扑图论的发展密切相关。

重构问题

1929年， S.M.乌拉姆提出了一个猜想：设图G＝(V， E)，H＝(V┡， E┡)，其中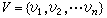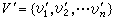，，且n≥3，对于i=1，2，…，n，若子图G_i=G-υ_i与H_i=H-υ媴同构，则图G与H同构，这是图论中著名的重构猜想，尚未得到证明。

邻接矩阵

对一个给定的n个点的图，构造一个n×n矩阵A=(α_ij)，其中所有α_ii=0；对于i≠j，且点υ_i与υ_j互相邻接，则取α_ij＝1；否则α_ii=0。该矩阵A=(α_ij)称为图的邻接矩阵。代数图论中很多结果是通过研究邻接矩阵获得的。基尔霍夫于1847年证明了如下的著名定理：矩阵M所有代数余因子都相等，且其值等于G的支撑树的数目，此处M=(m_ij)也是一个n×n矩阵，所有的m_ii＝d(υ_i)；当i≠j时，取m_ij＝-α_ij。

有向图

若将图G=(V，E)中E的元素都变成有序的点对（即给边规定了方向）， 则称此图为定向图。 人们常见的物资流向图、电流图、计算程序框图等都是属于定向图。定了向的边 e=(υ_i，υ_j)称为弧。而 υ_i称为弧的起点， υ_j称为弧的终点。以 υ为起点的弧的数目， 称为υ的出度;以υ为终点的弧的数目，称为υ的入度。若一点序列

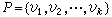中相继两点所构成的有序点对(υ_i，υ_j+1)都是定向图中的弧， 则称p为一条以υ₁为起点、υ_k为终点的定向链。一条起点和终点重合的定向链称为定向圈。若一个支撑树上的边的定向满足如下条件：有一个点的入度为零(称之为根)，其余各点的入度都是1，则此树称为定向树(或树形图)。如图10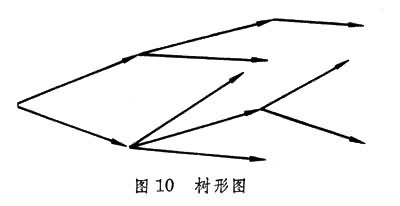

所示，图中箭头表示边的定向。 假如在任意两个点υ_i与υ_j之间，允许存在弧(υ_i，υ_j)和(υ_j，υ_i)，则称其为有向图。

定向图常常被用来描述元素间的某种偏序关系。例如表示人与人之间的上下级关系；比赛过程中的输赢关系;生产过程中工序的先后顺序；集合间的包含关系;状态间的转移关系；命题间的逻辑关系，等等。对有些物理和化学现象可以利用有向图来表示变量之间的函数关系。在图上，按一定的计算规则，就可直接求得问题的解答。在网络分析中，图论早已成为一种有力的工具。图论和线性规划相结合，产生了网络流理论和组合最优化，而成为运筹学中应用较广的两个分支。

参考书目

1. F.Harary，Graph Theory， Addison-Wesley， ReadingMass.， 1969.
2. C.Berge，Graphs and Hypergraphs， North-Holland，Amsterdam， 1973.
3. J.A.Bondу and U. S.R.Murty，Graph Theory with Applications， Macmillan， London， 1976.