整除

[拼音]：zhengchu

[外文]：divisibility

数论中一个最基本的概念。任给二整数α与b，其中b≠0，如果有一个整数с使 α=bс，就称b能整除α，记作b│α。此时把b叫作α的因数，α叫作b的倍数。如果b不能整除α，就记作b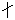α。通常，因数总假定是正的。从整除的定义出发，以下一些性质是明显的：

（1）若b│α，с│b，则с│α；

（2）若b│α，则сb│сα，反之亦然；

（3）若с│α，с│b，则对任意的整m，n，有с│mα+nb；

（4）若b｜α，则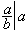。一般地，有所谓的带余除法，即设α、b是二整数，其中b>0，则存在两个惟一的整数q和r，使得α=bq+r，0≤r<b，r叫作α被b除所得到的余数，记为<α>_b=r显然，b)整除α当且仅当r=0。

最大公因数与辗转相除法

设α₁，α₂，…，α_n(n≥2)是n个整数，若整数d>0是它们之中每一个的因数，那么d就叫作α₁，α₂，…，α_n的一个公因数，诸公因数中最大的一个叫作最大公因数，记作 (α₁，α₂，…，α_n)。如果(α₁，α₂)=1，那么α₁和α₂叫做互素或互质。设α、b是任意两个正整数，由带余除法可得下列诸式：

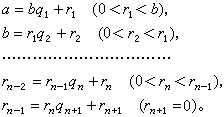
因为b>r₁>r₂>…，故经有限步之后，r_n+1=0，且(α，b)=r_n。这就叫做辗转相除法，又称欧几α₂，…，α_n的一个公倍数，所以最小公倍数总是存在的。设α、b是任意二正整数，则：

（1）α、b的所有公倍数就是[α，b)]的所有倍数；

（2）[α，b](α，b)=αb。

素数和算术基本定理

正整数可以分成三类；①1，只有正整数1是它的因数；

（2）素数p，p>1，只有正整数1和p是它的因数；

（3）复合数m，有大于1同时小于m的因数。欧几里得证明了素数的个数是无限的。因为，如果素数有限，设为p₁，p₂，…，p_k而整数p₁，p₂，…p_k+1中必有不同于 p₁，p₂，…，p_k的素因数。他还证明了若素数p│αb，则p│α或p│b。由此可得算术基本定理:任一大于1的整数数n，如果不计顺序，那么只有惟一的方法表示成素数的乘积里得算法，它是古希腊数学家欧几里得于公元前 4世纪给出的。他还证明了存在二整数l和m使得(α，b))=lα+mb)。显然，α、b)的任何公因数是(α，b)的因数。

最小公倍数

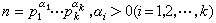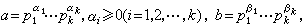
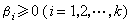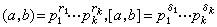设α₁，α₂，…，α_n(n≥2)是 n个正整数，如果m是这n个数中每一个数的倍数，那么m 就叫做这n个数的一个公倍数，一切公倍数中最小的正整数叫做最小公倍数，记为[α₁，α₂，…，α_n]。因为乘积α₁α₂…α_n就是α₁，。由这个定理可知，任一大于1的整数n可惟一地分解成标准形式 ，其中p₁<p₂<…<p_k是素数。作为算术基本定理一个简单而直接的应用，设，则，其中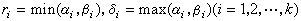。多于两个正整数的最大公因数和最小公倍数可以仿此求出。算术基本定理又叫整数的惟一分解定理，是数论中一个基本的定理，许多结果依赖于它的成立。代数数论研究的主要问题之一，就是研究在给定的代数数域中代数整数的惟一分解定理是否成立。

如何把一个给定的大的正整数分解为它的标准形式，一直是人们所关心和研究的问题，它不仅具有理论意义，而且有实际应用。虽然已经得到一些较有效的算法来判断一个大数是否素数，但是分解一个大数，仍然十分困难，即使借助于电子计算机也要花费惊人的时间。利用大数分解的困难性，1977年，R.L.里弗斯特等人设计出一种能够公开密钥的密码。

埃拉托斯特尼筛法

大约在公元前250年，古希腊数学家埃拉托斯特尼提出一个造出不超过N 的素数表的方法，它基于这样一个简单的性质:如果n≤N，而n是复合数，则n必为一不大于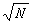的素数所整除。具体作法如下：先列出不超过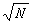的全体整数，设为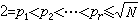，然后依次排列2，3，…，N，在其中留下p₁=2，而把p₁的倍数全划掉，再留下p₂，而把p₂的倍数全划掉，继续如此往下做，直到最后留下p_r而划去p_r的倍数。所留下的整数就是不超过N 的全体素数。这就是著名的埃拉托斯特尼筛法。近代素数表都是由此法略加变化造出。1914年，D.H.莱默尔发表了1到10006721的素数表。1951年，J.P.库利克等又增加了从10006721到10999997间的素数。最大的素数表是D.B.扎盖尔1977年发表的，列出了不超过5×10⁷的素数。埃拉托斯特尼筛法的改进和发展，是近代解析数论的重要工具之一。