整函数_自然百科

[拼音]：zhenghanshu

[外文]：integral function

整个复平面C内全纯的函数。根据外尔斯特拉斯，K.（T.W.）的观点，一个整函数ƒ(z)以任一点为中心的幂级数展式在整个复平面内收敛，因此无需进行解析开拓此展式即在整个C内代表此函数，并且显然是单值的。若整函数表示式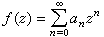中只有有限多个非零系数，则为一多项式，它是整函数的特殊情形，当p=0时，无穷远点是它的可去奇点；当p>0时，无穷远点是它的极点。若幂级数表示式中有无穷多个非零系数，则ƒ(z)为一超越整函数，它能看作是多项式的推广，无穷远点是它的本性奇点。例如，

是超越整函数。

整函数的因子分解

这是多项式因子分解定理在整函数中的推广，它首先由外尔斯特拉斯于1876年所建立。多项式最基本的性质（代数基本定理）是:p次多项式在复平面内恰有p个根（按重级计算）。多项式的次数p还给出函数模当z→∞时增长速度的量度，即有

。

根据上述代数基本定理，每一多项式有惟一的乘积表示，亦称因子分解，即

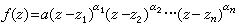
式中α为常数，{z_k}为零点，{α_k}为相应的重数。上面的表示式将多项式的零点位置和相应的重数明显地表示出来；反之，总能构造一多项式使得它具有预先给定的零点和重数，它表为乘积的形式，且除去一个常数因子外是确定的。对一般整函数能够提出相同的问题，但与多项式的情形有很大的差别。例如，若ƒ(z)有无穷多个零点{z_n}，设z_n≠0，但不一定是收敛的，它的值可能依赖于因子的排列顺序；再者，存在不取零值的整函数，所以整函数的零点还不能象多项式一样可以决定它的基本性质。为了保证无穷乘积收敛，须对每个因子进行适当的修改，外尔斯特拉斯定义初等因子

并且有下述定理。

外尔斯特拉斯第一定理

设：为整函数ƒ(z)的非零的零点，且满足，又设，为正整数列，使得级数对任一r为收敛，则无穷乘积

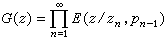(1)

对任意z绝对收敛，此时

， (2)

式中g(z)为另一整函数；m为某个非负整数。

值得注意的是这里{p_n}总是存在的，但不确定，因为任何更大的数列都能代替它。此外e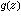亦不确定，且能任意快地增长。为了区分整函数的不同类，E.N.拉盖尔（1882）引进了格的概念，在某种意义下它类似于多项式的次数。设存在一数λ>0，使得收敛，则有一最小的整数k≥0，使得收敛。这时称为关于{z_n}的典型乘积，k称为它的格。此典型乘积是惟一确定的。若进一步假设 (2)中的g(z)是q次多项式，则称p=Max{k，q}为ƒ(z)的格。