概率分布

[拼音]：gail╇ fenbu

[外文]：probability distribution

概率论的基本概念之一，用以表述随机变量取值的概率规律。为了使用的方便，根据随机变量所属类型的不同，概率分布取不同的表现形式。

离散型分布与分布列

只取有限个或可列个实数值的随机变量称为离散型随机变量。例如，1000件产品中有50件次品，从中随意抽取100件，则其中的次品数X 就是一个只取 0到50之间的整数值的离散型随机变量。又如一个电话交换台每天收到的呼叫次数X 就是一个可取全部非负整数值的离散型随机变量。设离散型随机变量X所取的全部值为{x₁，x₂，…，x_n，…}，记事件{X=x_k}的概率P(X=x_k)=p_k，k=1，2，…，n，…，于是二元序列{(x_k，p_k)，k=1，2，…，n，…}表述了X取值的概率规律。这个二元序列称为分布列。可用分布列来表述的离散型随机变量取值的概率规律称为离散型分布。由概率的基本性质可知，任一分布列必然满足条件:p_k≥0，（若随机变量只取n个值，则有)。

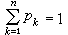上述表达形式也适用于随机向量的情形，这只须把X理解为m 维随机向量X =(X₁，X₂，…，X_m)，x_k理解为m 维向量值，事件{X=x_k}的概率p_k理解为 。相应的分布列所表述的概率规律称为m 维离散型分布。

分布函数与边缘分布函数

对于那些取值充满一个区间[α，b]、 甚至充满整个实数轴R=(-∞，∞)的随机变量，就不可能用分布列的形式来表述它取值的概率规律，一般可统一用分布函数来表述。设X是一个随机变量，x是任一实数，事件｛X≤x｝的概率P(X≤x)=F(x)，x∈R，称为X的分布函数;在数理统计学中也称为累积分布函数。由概率的性质知道，任何分布函数F(x)都满足以下三个条件：

（1）单调非降，即当α<b时，F(α)≤F(b)；

（2）右连续，即，其中b→α+表示b>α且趋近于α；

（3），。反之，任一满足这三个条件的函数，必是某一随机变量的分布函数。用分布函数可以表示X落入某个区间的概率，例如当α<b时，P(α<X≤b)＝F(b)-F(α)，P(α≤X≤b)＝F(b)-F(x)=F(b)-F(α-)。图1画出了一个分布函数的图像。

如果X是一个离散型随机变量，它的分布列为{(x_k，p_k)，k=1，2，…，n，…}，那么由概率的可列可加性知道，X的分布函数可以表为 其中右边的求和式表示对满足 x_k≤x的一切下标k求和。图2画了一个这种类型的分布函数。

分布函数的定义也容易推广到随机向量的情形。设X=(X₁，X₂，…，X_m)是一个m 维随机向量，x=(x₁，x₂，…，x_m)是任一m 维实向量，令 ，则函数F(x₁，x₂，…，x_m)称为X 的m 维分布函数，或称为m个随机变量X₁，X₂，…，X_m的联合分布函数。m 维分布函数也有与一维情形相应的充分必要条件，但叙述较为复杂。

利用X₁，X₂，…，X_m的联合分布函数F(x₁，x₂，…，x_m)，可以求出其中任何一部分随机变量的分布函数，后者称为前者的边缘分布函数。以两个随机变量X₁、X₂为例，设它们的联合分布函数为F(x₁，x₂)，则X₁，X₂的两个边缘分布函数分别为

及

。

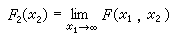连续型分布与密度函数

实际中最常遇到的随机变量的类型除离散型以外，还有连续型随机变量。如果存在一非负实函数p(x)，使随机变量X的分布函数F(x)可以表成：

，

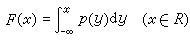则称X为连续型随机变量，p(x)称为X 的密度函数，它一定满足条件

。

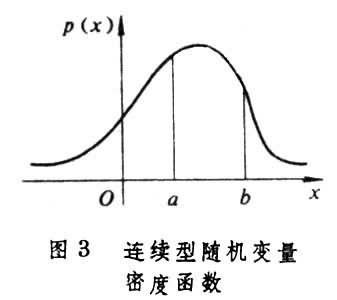
可以用密度函数来表述的随机变量取值的概率规律称为连续型分布。连续型随机变量 X取任何一个实数值的概率等于0；当实数α<b时，可以用密度函数在区间[α，b]上的积分计算事件｛α≤X≤b｝的概率，即:

，

这个概率又可以用图3中阴影部分的面积来表示。

如果存在一个m元实函数p(x₁，x₂，…，x_m)，使m 维随机向量X＝(X₁，X₂，…，X_m)的分布函数F(x₁，x₂，…，x_m)可以表示成

，

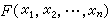
则p(x₁，x₂，…，x_m)称为随机向量X 的m 维密度函数，或称为m个随机变量X₁，X₂ ，…，X_m的联合密度函数。若两个随机变量X₁，X₂有联合密度函数p(x₁，x₂)，则X₁、X₂自身也分别有密度函数p₁(x₁)和p₂(x₂)，且可以由下式算出：

，

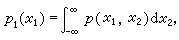
p₁(x₁)，p₂(x₂)分别称为p(x₁，x₂)的边缘密度函数。类似地，可以考虑m　维密度函数的边缘密度函数。

概率分布的测度形式

有时，主要是为了理论研究的方便，还需要有一种表述随机变量与随机向量取值的概率规律的更一般的形式。对给定的正整数m，用R^m表示全体m 维实向量构成的集，称为m 维实空间，对于α=(α₁，α₂，…，α_m)，用符号(α，b]表示R^m中如下的超长方体：(α，b]={x∈R^m:x=(x₁，x₂，…，x_m)，α_j<x_j≤b_j(j=1，2，…，m)，又用B^m表示由R^m中的一切超长方体产生的σ域，称为m维波莱尔域，B^m中的成员称为R^m中的波莱尔集。由随机变量的公理化定义可知，若X为概率空间(Ω，F，P)上的m 维随机向量，则对任一B∈B^m有{X∈B}∈F。对每一B∈B^m，定义P_X(B)=P(X∈B)，则P_X是可测空间(R^m，B^m)上的一个概率测度（见概率）。这个概率测度P_X一般也称为随机向量X 的概率分布。

实际上，对于不同类型的随机变量X，它的概率分布P_X分别被它的分布列、密度函数和分布函数完全确定。以一维情形(m=1)为例，对于任一B∈B¹，其P_X(B)分别为：

式中最后一个积分是勒贝格-斯蒂尔杰斯积分。

随机变量的函数的分布

一个或多个随机变量的连续函数或初等函数（甚至更一般的波莱尔可测函数）仍然是随机变量，而且后者的分布由前者的分布完全确定。这一事实无论在理论上或实际计算上都是重要的。例如，设随机变量X的分布函数为F(x)，α(>0)及b是二实数，则Y=αX+b也是随机变量，它的分布函数

。

又如随机变量X₁，X₂有联合密度函数p(x₁，x₂)，则X=X₁+X₂及Y=X₁/X₂也是随机变量（在后者中，假定X₂≠0)），它们分别有密度函数

及

。

数学期望

见数学期望。

方差

见方差。

中位数与分位数

设X是随机变量，同时满足P｛X≤x｝≥1/2及P｛X≥x｝≥1/2二式的实数x，称为X的中位数，记作m_X或x_1/2。中位数对于任何随机变量都是存在的，但可能不惟一。它是反映随机变量取值中心的一个数值。在理论上，特别对数学期望不存在的情形，它可以起到类似于数学期望的作用。它与期望相比，主要优点是受极端值的影响较小，因此在某些应用统计问题中，用它代替平均数作为一个主要指标。

将中位数的概念推广，可以引进数理统计学中常用的分位数的概念。给定0<α<1 ，随机变量X的上α分位数是指同时满足下列两条件的数x_α：P｛X≤x_α｝≥1－α，P｛X≥x_α｝≥α。中位数就是1/2分位数。x_1-α 又称为X的下α分位数。

特征函数

傅里叶变换是数学分析中非常重要而有效的工具，将它应用于概率论，对分布函数作傅里叶-斯蒂尔杰斯变换，就得到特征函数。由于它具有很好的性质，因此在研究随机变量之和及其概率分布时起着十分重要的作用。在P.莱维于1919年至1925年系统地建立概率论中的特征函数性质以后的15年间，它被用来完整地解决了普遍极限定理（见中心极限定理），并深入地研究了独立增量过程。

设F(x)是随机变量X的分布函数，则称

(t∈R)为F(x)或X 的特征函数。特别，若分布是具有密度函数p(x)的连续型分布，则

；

若分布为

P(X =x_k)=p_k (k=1，2，…)，的离散型分布，则

。

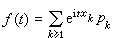特征函数的重要性质有：

（1）ƒ(0)=1；

（2）│ƒ(t)│≤1，t∈R；

（3）ƒ(t)在R上一致连续且具有非负定性，即对任意正整数n，任意实数t₁，t₂，…，t_n，及任意复数 z₁，z₂，…，z_n，有；

（4）若X的r阶绝对矩有穷，则对一切正整数 k≤r，它的特征函数的k阶导数存在，且 因而有 在特征函数已知的情况下，用这类公式来求各阶矩往往是方便的。如果随机变量 X₁，X₂，…，X_n是独立的，则X₁＋X₂＋…＋X_n的特征函数等于 X₁，X₂，…，X_n各自的特征函数的乘积。这一性质使特征函数在研究极限定理（见中心极限定理）时起着重大的作用。

特征函数与分布函数相互惟一决定，因而可以把求分布函数的问题转化为求特征函数的问题。不仅如此，在特征函数序列与分布函数序列的收敛性之间也存在对应关系。称分布函数序列{F_n(x)，n≥1}弱收敛（见概率论中的收敛）于分布函数F(x)，如果在F(x)的每一连续点x上，都有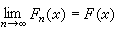。于是，成立如下的定理：设分布函数序列{F_n(x)}弱收敛于分布函数F(x)，则相应的特征函数序列{ƒ_n(t)}收敛于F(x)的特征函数ƒ(t)，而且在t的任一有限区间上收敛是一致的。反之，设特征函数序列收敛于一个在t=0处连续的函数ƒ(t)，则ƒ(t)是特征函数，而且相应的分布函数序列弱收敛于以ƒ(t)为特征函数的分布函数F(x)。这是解决中心极限问题时的一个关键性的定理。应用它，还可以证明：R上的复值函数ƒ(t)为特征函数的充分必要条件是ƒ(t)连续、非负定且ƒ(0)=1。这是特征函数的一个判定条件，而且在证明平稳过程协方差函数的谱表示时需要用到这个定理。

上述有关一维概率分布的特征函数的概念与结果，都可以推广到多维的情形。

半不变量

设随机变量X具有s阶绝对矩，则它的特征函数ƒ(t)s次连续可微，令

，

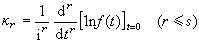它称为X的r阶半不变量。因此有

，

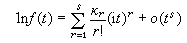式中符号O(t^s)表示当t→0时比t^s高阶的无穷小量，即X 的前几阶半不变量是：

…………。

给定前两阶半不变量 k₁、 k₂，其最简单的特征函数是exp，即正态分布N(k₁，k₂)的特征函数。

母函数

它是代替特征函数专门用于研究非负整值随机变量的一个有用的数学工具，历史上，它的引进比特征函数更早。设 X是只取非负整数值的离散型随机变量，P(X=k)=p_k，k=0，1，…，则称

为X 或其概率分布的母函数。由幂级数的求导性质知，P(s)在(-1，1)中有任意阶导数，且p_k=(0)/k!，k=0，1，…，因此，母函数与取非负整值的离散型分布相互惟一决定。母函数还具有如下的重要性质：当X 的数学期望存在时，EX=P′(1)；当X的方差有穷时，;任意n个独立的非负整值随机变量之和的母函数，是这n个随机变量的母函数的乘积；设v及X₁，X₂，…是一列独立的非负整值随机变量，而且 X₁，X₂，…有相同的概率分布，其共同的母函数为 P(s)，v的母函数为G(s)，则随机变量的母函数为G(P(s))；此外，若Ev及EX₁存在，则EY=Ev·EX₁。

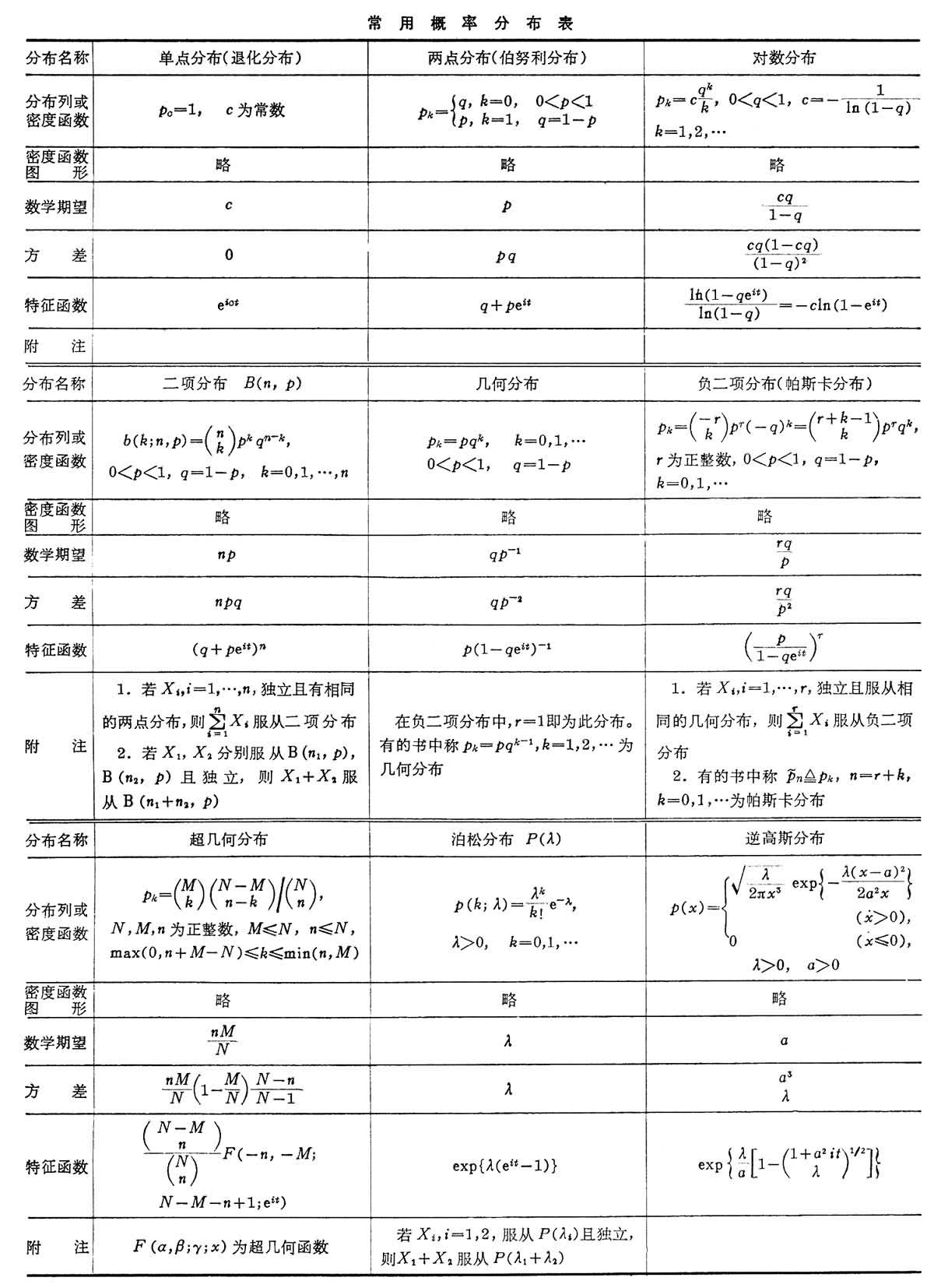
常用概率分布表

表列举了概率论与数理统计学中常用的概率分布(包括取整数值的离散型分布及连续型分布)，它们的名称与标准记号，分布列或密度函数表达式及部分密度函数的图形，相应的数学期望与方差(如果存在)，以及相应的特征函数。另外，还加了若干有用的附注。表中的X～N(α，σ²)表示随机变量X服从期望为α、方差为σ²的正态分布。

参考书目

1. J.K.Patel，C.H.Kapadia and D.B.Owen，Handbork of Statistical Distributions，Marcel Dekker，New York，1976.