[拼音]:zhengshu guihua
[外文]:integer programming
一类要求变量取整数值的数学规划。若要求全部变量取整数值,则称为纯整数规划,简称为整数规划。若只要求部分变量取整数值,则称为混合整数规划。特别地,当在线性规划中要求变量取整数时,就是线性整数规划。若要求变量为0,1变量,即其值只取0或1时,则称为 0-1规划。由于实际问题中有许多量具有不可分割的性质,如人数、机器数、元件数等;还有一些逻辑现象如开与关,取与舍,有与无等可利用0、1变量作数量化描述,因此,在线路设计、工厂选址、人员安排、代码选取以及其他领域中,常常出现整数规划问题。1958年,R.E.戈莫里提出解线性整数规划的割平面法后,整数规划逐步形成一个独立的分支。
形式最简单的整数规划问题是背包问题,也就是求 max ,满足
,满足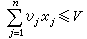 (xj取0或1)的解的问题。假如将V 解释为背包的容积,vj为物体j的体积,wj为物体j的重量,而变量xj取1时表示物体j装入背包,xj取0时表示物体j不装入背包,那么背包问题就是要寻求一种既不超过背包容积,又能使总重量最大的装法。背包问题的一种特殊解法是动态规划的方法,这种方法所需的计算时间与所给问题中的参数n,V有关,大致与nV成正比例增长。
(xj取0或1)的解的问题。假如将V 解释为背包的容积,vj为物体j的体积,wj为物体j的重量,而变量xj取1时表示物体j装入背包,xj取0时表示物体j不装入背包,那么背包问题就是要寻求一种既不超过背包容积,又能使总重量最大的装法。背包问题的一种特殊解法是动态规划的方法,这种方法所需的计算时间与所给问题中的参数n,V有关,大致与nV成正比例增长。
设所给的整数规划问题(p)为求极小值问题。在整数规划的一般性解法中,有三个基本概念。
(1)分解,以F(p)表示问题(p)的约束集。所谓问题(p)分解为子问题(p1),(p2),…,(pq)之和,是指满足条件(S1)和(S2),(S1):问题(p)的任何一个可行解,恰好是(p1),(p2),…,(pq)中某一个问题的可行解;(S2):任何子问题(pi)的可行解也是(p)的可行解,即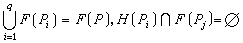 ,1≤i≠j≤q。最通常的分解方式是“二分法”,例如,若xj是(p)的0,1变量,把条件“xj=0”和“xj=1”分别添进问题(p)的约束条件中,则问题(p)分解为两个子问题之和。
,1≤i≠j≤q。最通常的分解方式是“二分法”,例如,若xj是(p)的0,1变量,把条件“xj=0”和“xj=1”分别添进问题(p)的约束条件中,则问题(p)分解为两个子问题之和。
(2)松弛,凡是放弃问题(p)的某些约束条件后所得到的问题(慉),都称为问题(p)的松弛问题。任何松弛问题(慉)都具有以下三个明显的性质:(R1)若(慉)没有可行解,则(p)也没有可行解;(R2)对同样的目标函数而言,(p)的最小值不小于(p)的最小值;(R3)若(慉)的一个最优解是(p)的可行解,则它也是(p)的一个最优解。最通常的松弛方式是放弃变量的整数性要求。
(3)探测假设按某种规则,已将问题(p)分解为子问题(p1),(p2),…,(pq)之和,并且各 (pj)已有对应的松弛问题(慉j)。若(慉j)没有可行解,则探明了(pj)没有可行解,因此,可从(p)的分解表上把它删去。此种情形记为 (F1)。假若当时已掌握了(p)的一个可行解尣*,与之相应的目标函数值为z*,如果松弛问题(慉j)的最小值不比z*小,那么就探明了(pj)中没有比尣*更好的可行解,因此已无须再考虑子问题(pj),就可从分解表上把它删去。此种情形记为(F2)。若(慉j)的最优解是(pj)的可行解,则已求得了(pj)的一个最优解。因此也无须再考虑它了,可以从分解表上把(pj)删去,这时若(pj)的最优解比尣*好,则替换掉尣*,同时刷新z*的值。此种情形记为(F3)。假如各个(慉j)的目标函数最小值都不比z*小,则尣*便是原问题(p)的最优解。此种情形记为 (F4)。情形 (F1)通常称为可行性探测。情形(F2)至(F4)通常称为最优性探测。
概括地说,求解一个整数规划问题(p),有以下几个步骤。首先,选定一种松弛方式,将(p)松弛为问题(慉),使得比较容易求解。若(慉)没有可行解,则(p)也没有可行解。若(慉)的最优解是(p)的可行解,则已求得(p)的最优解。若(慉)的最优解不是(p)的可行解,则有两条不同的途径,一是设法改进松弛问题(慉),继续探测问题(慉);一是选定一种分解方式,把(p)分解成两个或几个子问题之和,将其列表记录,并且赋予各子问题尽可能好的目标函数值的下界。然后,按一定的次序,逐个进行探测。当某个子问题已经被探明时,就从表中删去,否则,继续对子问题进行分解。
对线性整数规划问题,不用分解的算法有割平面法,它以线性规划问题作为松弛问题,利用生成割平面来不断改进松弛问题,使最终求得的松弛问题的最优解也是整数解;还有一种是群论方法,它用有限阿贝尔群上的一个背包问题作为松弛问题,是放弃一部分变量的非负性要求后得到的。利用分解的算法有隐数法和分枝定界法两类。它们通常都是以线性规划问题作为松弛问题,不同之处仅在于探测子问题的先后次序。隐数法是按照子问题表中“先入后出”的原则来确定探测次序,即后出现的子问题先探测。分枝定界法是按照所赋予的下界大小来确定探测的先后顺序,即下界小的子问题优先探测。前者计算程序比较简单,在计算过程中所需要保存的信息较少,而后者在选取子问题时有灵活性,因为往往下界数值小的子问题中存在最优解的可能性较大。
对线性混合整数规划问题,J.F.本德尔斯提出了一种分解算法。它的求解过程可以分为两部分,一部分是解一个线性整数规划问题,另一部分是解一个线性规划问题。
割平面法例如,考虑整数规划问题:求
 (1)
(1)
满足条件
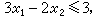 (2)
(2) (3)
(3)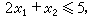 (4)
(4) (5)x1、x2取整数值。 (6)
(5)x1、x2取整数值。 (6)
取它的松弛问题为线性规划(1)~(5),约束集为图1

中的多边形ABCD。整数规划的可行解是此多边形内的整点(即座标为整数的点)。松弛问题的基本最优解为
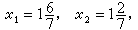
即图1中的点C。目标函数的最优值
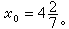
设
 (7)
(7) (8)
(8)
从(7)和(8)中解出x1、x2,得
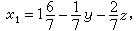 (9)
(9) (10)
(10)
因x1、x2、y、z都必须取整数值,故由(9)和(10)可得同余方程
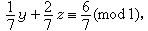 (11)
(11)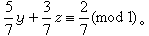 (12)
(12)
利用方程(11)或(12)中y和z的系数,可以导出整数规划的一个新的约束条件,例如,用
 乘条件(2)的两边,用
乘条件(2)的两边,用 乘(4)的两边,然后将(2)和(4)的两边分别相加,可得
乘(4)的两边,然后将(2)和(4)的两边分别相加,可得 。由于 x1必须取整数值,就可推得一个新的约束条件:x1≤1。这就是整数规划的一个割平面。类似地,由
。由于 x1必须取整数值,就可推得一个新的约束条件:x1≤1。这就是整数规划的一个割平面。类似地,由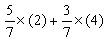 可推得另一个割平面:3x1-x2≤4。增加割平面 x1≤1后,新的松弛问题的约束集如图2
可推得另一个割平面:3x1-x2≤4。增加割平面 x1≤1后,新的松弛问题的约束集如图2
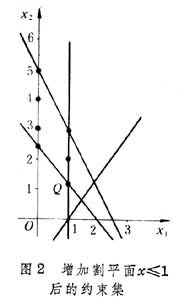
所示。它的基本最优解为:x1=1,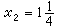 ,是图2中的点Q。
,是图2中的点Q。 再由条件x1≤1和
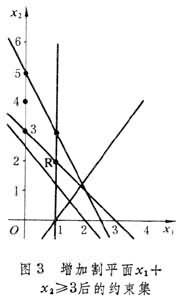
再由条件x1≤1和 可导出一个新的割平面:x1+x2≥3。增加此割平面后,松弛问题的约束集如图3所示。它的基本最优解为:x1=1即图3中的点R。由于它已是整数解,故必为整数规划(1)~(6)的最优解。目标函数的最大值x0=1。
可导出一个新的割平面:x1+x2≥3。增加此割平面后,松弛问题的约束集如图3所示。它的基本最优解为:x1=1即图3中的点R。由于它已是整数解,故必为整数规划(1)~(6)的最优解。目标函数的最大值x0=1。
例如,整数规划问题(p):求
 (13)
(13)
满足条件
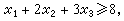 (14)
(14)
 (15)
(15)
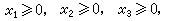 (16)
(16)
x1、x2、x3取整数值。 (17)
取松弛问题(慉)为线性规划(13)~(16)。(慉)的最优解为 x1=0.4,x2=3.8,x3=0;x0=14.2。按条件x2≤3和x2≥4将 (p)分解为子问题(p1)与(p2)之和。解(p1)的松弛问题(慉1),得尣1:x姌=0.5,x姟=3,x
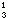 =0.5;x姲=14.5。再按条件x1=0和x1≥1将(p1)分解为(p3)与(p4)之和。这时子问题表为{(p3,(p4),(p2)}。这些子问题的x0的下界,暂时都可以取为15。按表中“先入后出”原则,解(p3)的松弛问题(慉3),得尣3:x婤=0,x婦=3,x婫=2;x庎=17。由于尣3是整数解,故必为(p3)的最优解。因此,(p3)已被探明,就可从表中删去,记尣*=尣3,z*=17,这是被找到的第一个整数解。解(慉4),得
=0.5;x姲=14.5。再按条件x1=0和x1≥1将(p1)分解为(p3)与(p4)之和。这时子问题表为{(p3,(p4),(p2)}。这些子问题的x0的下界,暂时都可以取为15。按表中“先入后出”原则,解(p3)的松弛问题(慉3),得尣3:x婤=0,x婦=3,x婫=2;x庎=17。由于尣3是整数解,故必为(p3)的最优解。因此,(p3)已被探明,就可从表中删去,记尣*=尣3,z*=17,这是被找到的第一个整数解。解(慉4),得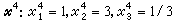 ;
; 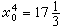 。由于x
。由于x z*=17,故已探明(p4)中没有(p)的最优解。解(慉2),得
z*=17,故已探明(p4)中没有(p)的最优解。解(慉2),得 。按条件x1=0和x2≥1 将(p2)分解为(p5)与(p6)之和。(p5)、p6的x0的下界可取为15。解(慉5),得
。按条件x1=0和x2≥1 将(p2)分解为(p5)与(p6)之和。(p5)、p6的x0的下界可取为15。解(慉5),得
 。由于尣3是整数解,故已探明(p5)。由于x
。由于尣3是整数解,故已探明(p5)。由于x <z*=17,故可刷新记录解,取尣*=尣3,
<z*=17,故可刷新记录解,取尣*=尣3,
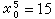 。由于x
。由于x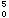 也达到(p6)的下界,故已探明(p6)中没有比尣3更好的解,至此(p)已探明,最优解为尣*=尣3。以上过程可表示为图4
也达到(p6)的下界,故已探明(p6)中没有比尣3更好的解,至此(p)已探明,最优解为尣*=尣3。以上过程可表示为图4
。
- 参考书目
- R.S.Garfinkel and G.L.Nemhauser,Integer Programming, John Wiley & Sons, New York,1972.