大范围变分法

浏览

[拼音]：dafanwei bianfenfa

[外文]：calculus of variations in the large

用拓扑方法研究变分问题的数学分支。古典的变分法研究泛函的极值──极大值或极小值。然而物理、几何以及分析中提出的变分问题，一般不仅要研究泛函的极值点，而且还要研究其临界点，即其变分为零的点。大范围变分法就是研究临界点的理论。

假设M是一个微分流形，ƒ是M上的光滑函数，所谓一点p∈M是ƒ的临界点，是指ƒ的导映射dƒ在这点为零。ƒ在临界点处的值，称为临界值。对任意实数α，称ƒα={p∈M|ƒ(p)≤α}为函数ƒ的水平集。大范围变分法的基本手法是通过考察拓扑空间ƒα随α变化时，其拓扑结构的变化，来判定临界点的存在性和估计临界点的个数。下面是一个有启发性的例子。考察切于平面π的一个环面M，如图

图

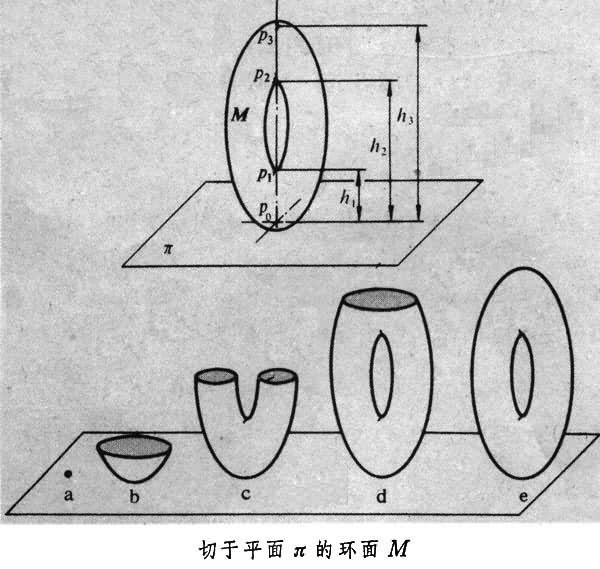
所示。

设ƒ:M→R1是关于平面π的高度，易见：

（1）当α<0时，ƒα=═，②当α=0时，ƒα={p0}，如图之a，③当0<α<h1时，ƒα如图之b，④当h1<α<h2时，ƒα如图之c，⑤当h2<α<h3时，ƒα如图之d，⑥当α≥h3时，ƒα＝M，如图之e。其中 hi=ƒ(pi)(i=1，2，3)，连同极小值0，都是ƒ的临界值。这个例子表明：若在实数α，b(α<b)之间没有ƒ的临界值，则ƒα与ƒb是同胚的， 但当α越过ƒ的一个临界值时，一般地，ƒα的拓扑结构将发生变化。这就是大范围变分法的基本出发点。

H.M.莫尔斯考察了非退化函数的临界点的性态与紧流形M本身的拓扑结构间的联系。函数ƒ称为是非退化的，是指在它的所有临界点上，对应的由二阶导数构成的黑塞矩阵 (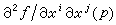)都是非退化的。对应的黑塞矩阵的负本征空间的维数，称为这临界点的莫尔斯指数。用Mk表示函数ƒ的莫尔斯指数为k的临界点的个数。莫尔斯理论的核心是下列莫尔斯不等式：

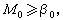
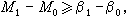
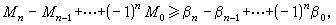
式中βk是流形M的贝蒂数。应用这组不等式于上例，因为环面有贝蒂数β0=β2=1，β1=2，所以得出：ƒ至少有4个不同的临界点。

基于类似的基本思想，Л.Α.柳斯捷尔尼克、Л.Γ.施尼雷尔曼开辟了另一条估计临界点个数的途径。对M上任意闭子集A，称A在M中的畴数为m，记作Cat(A)=m，是指A可以被m个可缩闭集所覆盖，但不能被m-1个这样的集合覆盖。畴数是一个拓扑不变量。为估计紧流形M上的函数ƒ的临界点个数有下界Cat(M)，柳斯捷尔尼克、施尼雷尔曼引进了下述重数定理：设

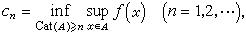
则当с=сm+1=…=сm+k时，ƒ的以с为临界值的临界点集K0有畴数Cat(K0)≥k。上例中的环面的畴数是3，所以环面上的任意函数至少有3个不同的临界点。柳斯捷尔尼克-施尼雷尔曼理论较莫尔斯理论适用范围宽，例如，函数ƒ不必是非退化的；但畴数的估计比较困难。

R.S.帕莱斯和S.斯梅尔把莫尔斯理论及柳斯捷尔尼克-施尼雷尔曼理论中流形M的紧性条件去掉，代之以在函数ƒ上添加帕莱斯-斯梅尔条件，即对于M上的任意点列{pn}，条件ƒ(pn)有界，连同dƒ(pn)→θ，蕴涵了{pn}有子列收敛。

莫尔斯理论以及柳斯捷尔尼克－施尼雷尔曼理论都被成功地应用到许多变分问题中去，特别是应用于研究黎曼流形上的闭测地线的个数，以及杨-米尔斯方程。

A.阿姆布罗塞蒂、P.H.拉宾诺维茨发展了柳斯捷尔尼克-施尼雷尔曼的思想，提出了山路引理:设ƒ是巴拿赫空间X上的一个满足帕莱斯-斯梅尔条件的C1函数，又设有θ的一个开邻域U和一点x0唘U，使得ƒ(θ)=ƒ(x0)=0，且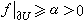，则ƒ至少有一个临界值с≥α。随后拉宾诺维茨又提出一系列极小极大原理。对许多由方程引出的变分问题的解的存在性以及个数估计有广泛的应用。特别是对哈密顿方程组周期解的存在性以及周期轨道个数的估计引出重要的结果。

参考书目
  1. R. Bott，Morse Theory，Old and New，BAMS，1981.
  2. W. Klingenberg，Lectures on Closed Geodesics，Springer Verlag， Berlin，1978.
  3. J. Milnor，Morse Theory， Princeton Univ. Press，Princeton，1963.
  4. M. Morse，The calculus of Variations in the large，American Math. Soc. Colloq.Pub.，New York，1934.
阅读全文