[拼音]：shulun bianhuan
[外文]：number-theoretic transform
在快速傅里叶变换(FFT)中，变换因子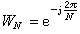
是一个复数，因而需要进行复数运算。但是，
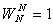，这表明WN是1的N次根。对于任意整数k，
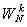是按k对N取模呈现周期性。在数论变换中，是以整数a代替复数WN实现正变换和反变换，要求这个整数是1的N次根。这一要求在一般的整数运算规则中不成立，只有采用同余式的运算规则才能找到满足这一要求的a和N。利用这样的a和N可以构成数论变换公式为
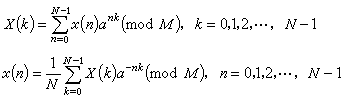(1)
显然，这种变换在计算速度上比快速傅里叶变换快。
把一个给定的正整数M称为模(mod)，如果用M去除任意两个整数α和β，所得余数相同，便称作α和β对模M同余，记作α 呏β(modM) (2)
因此，同余式运算规则是以正整数M为模的整数环（域上所定义的一种线性正交变换。
在式(1)中，整数a、N、M三者之间必须满足如下关系：aN呏1(modM) (3)
满足上式的最小正整数N叫做a对模M的指数，a是1的N次根，或简称a是N 阶的。例如，a为2时对模7的指数是3，对模11的指数是10。
在数论变换中要求找到合适的a、N和M值。所选择的N应当是高复合数。但如采用2的乘方，就能构成像FFT算法那样的信号流图，并且希望选取的N值足够大，以满足实际需要。其次，所选取的a应当能用简便的方法实现乘法运算，因为在计算机中乘法运算最花费时间；如果a是2的乘方，可以用移位操作实现a的乘方运算，因而比较方便。又由于是模运算，所以不存在舍入误差。此外，M最好也是位数不太多的二进制数，而且必须是大于2的素数。
麦森数论变换
在数论变换的一般公式 (1)中的模M采用麦森数时，就称为麦森数论变换。麦森数为M=2k－1 (4)
它是一奇数。令k=PQ，P为素数，便有
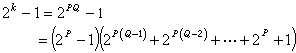
在此情况下，最大可能的变换长度决定于（2P-1）。以(2P－1)为模，可以找到
（1）a＝2，N＝P，aN＝2P呏1[mod(2P－1)]，但P是素数，N=P也是素数，不是高复合数。
（2）a＝－2，N＝2P，(－2)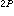
呏1[mod(2P－1)]，但由于N=2P，故不是高的复合数。因此，取麦森数作模是不合适的。
费马数论变换
在数论变换中比较合理的模M是选用费马数，即Ft=2b+1 b=2t (5)
前几个Ft的值是F0=3;F1=5;F2=17;F3=257；F4=65537；这五个费马数都是素数，而F5和F6都是复合数：F5=4294967297=641×6700417F6=274177×67280421310721在t＞4的情况下，还没有发现一个费马数是素数。Ft称为第t个费马数，模Ft的计算可用b位算术运算来完成。信号所占用的位数和滤波器系数决定了在输出中不引起溢出误差所需用的b值，实际用的b值比信号所占用位数的两倍稍大。为了能够采用费马数，如果以溢出条件得到的b值不是一个2的幂时，应该把它增加到接近的2的幂数。
因为是按模M=Ft费马数进行算术运算，所以长为N=2m的序数的费马数论变换及其反变换表达式可写成
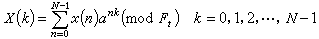
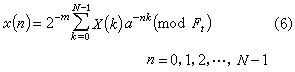
其中N是满足式aN呏1(mod Ft) (7)
的最小正整数。
费马数论变换和傅里叶变换相类似。当N =2m时，数论变换的快速计算法的信号流图和 FFT的算法信号流图也是一致的，只是把WN换成a。但是，费马数论变换的基本函数是由2的方幂构成，不需要使用乘法，仅为移位操作，其运算速度快于 FFT算法。加上费马数论变换算法是模算术运算，不存在舍入误差，从而能得到高精度的褶积。此外，由于FFT的基本函数是三角函数，需要预先存储这些基本函数，而费马数论变换算法却不需要存储基本函数。费马数论变换的缺点主要是它没有物理意义，在信号处理中不能运用中间过程；运算需要的字长与变换点数之间存在着严格的关系，随着输入序列的增长往往需要很长的字长。